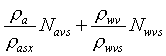 (1)
(1)
Abstract
This ad-hoc working group of the IAG Special Commission (SC3) has carefully reviewed the progress in the measurement and modelling of the refractive index of air. For light and near infrared waves, a closed simple formula is proposed for electronic distance measurement (EDM) to not better than one part per million (1 ppm) precision. For EDM of higher precision, a computer routine is proposed that uses the full Lorentz-Lorenz relationship, the new temperature scale of 1990, the BIPM density equations and the recently revised water vapour refractivity. The group notes that the perceived accuracy of any continuum formula is invalidated by anomalous refractivity near absorption lines. Further work on the effect of absorption lines on the phase and group refractive indices of air is strongly recommended, as are new absolute measurements of the refractivity of the constituent gases of the atmosphere (including water vapour) at non-laboratory conditions.
1. Introduction
In 1991, at the 20th General Assembly of the International Association of Geodesy (IAG) in Vienna, it was suggested that new IUGG resolutions on refractive indices be prepared for adoption at a future General Assembly of IUGG. An Ad-hoc Working Party on Refractive Indices of Light, Infrared and Radio waves in the Atmosphere was formed in 1993 under the umbrella of the International Association of Geodesy (IAG) Special Commission SC3 – Fundamental Constants (SCFC).
The last resolutions of the International Union of Geodesy and Geophysics (IUGG) on refractive indices date back to 1963. For light waves, the 1963 IUGG resolution recommended two interchangeable formulae for standard air by Barrell & Sears (1939) and Edlén (1953) as well as a simplified interpolation formula to ambient condition based on Barrell & Sears (1939). (To recommend two competing formulae was not such a good idea, considering that uniformity was to be achieved.) The formulae provided group refractive indices accurate to 0.1 ppm at standard conditions for carrier wavelengths between 185 and 644 nm. They were thought to give an accuracy of 2 ppm at ambient conditions. This was appropriate in 1963 when electro-optical distance meters were specified at ±(10 mm + 2-5 ppm). Today, the best commercial electro-optical distance meters have a precision of ±(0.1 mm + 0.1 ppm). Also, the state-of-the-art measurement of atmospheric parameters gives computed refractive indices with standard deviations of 1 to 5´10-8 (see Matsumoto et al. 1988, Birch & Downs 1993, for example). The formulae adopted in 1963 are not accurate enough for today's precision measurements, do not include post 1953 refractivity measurements and have not been designed for the near infrared spectrum where most distance meters operate today. This situation has led to the use of a variety of "non-approved" formulae in geodesy and surveying.
This report summarises the activities of the Ad-Hoc Working Party of the IAG Special Commission SC3 – Fundamental Constants (SCFC) for the period 1993 to 1999. In short, the working party was considering recent determinations of the refractive index of air, the carbon dioxide content of air, the extension of the formulae into the infrared and the implementation of the Lorentz-Lorenz relationship. So far, the working party concentrated on the refractive index in the visible and near infrared spectrum, because of an apparent lack of interest from geodesists working with GPS and VLBI. Work on proposals for refractive index formulae for the radio and millimetre waves has started, however, and some suggestions have been arrived at.
Three resolutions have been prepared by the working party for adoption at the 22nd General Assembly of IUGG (1999). They are reprinted in the Appendix. The first resolution recommends two solutions for the refractive index of light and near infrared waves, namely a simple closed formula (for the reduction of measurements of not better than one part per million) and a computer routine (for the reduction of measurements to better than one part per million). The second resolution makes recommendations on further work on the refractive index of light and infrared waves, with special emphasis on anomalous refractivity due to absorption lines. The third resolution recommends further work on the refractive index of infrared and radio waves.
The views expressed in this report are those of the author, but are based on consultations with the members of the group. The working party plans to publish a joint paper on its work soon. The extensive literature section includes references mentioned to in the text as well as other literature relevant to the work of the group.
2. Membership
Jean M. Rüeger (School of Geomatic Engineering, University of New South Wales, Sydney NSW 2052, Australia, e-mail: J.Rueger@unsw.edu.au), convener;
Philip E. Ciddor (National Measurement Laboratory, CSIRO, P.O. Box 218, Lindfield NSW 2070, Australia, e-mail: pec@dap.csiro.au);
Michael G. Cotton (Institute of Telecommunication Sciences, NTIA/ITS.S3, 325 Broadway, Boulder CO 80303, USA, e-mail: mcotton@ntia.its.bldrdoc.gov);
Yuri S. Galkin (Ecological Laboratory, Department of Physics, Moscow State University of Forestry MGUL, Mytischy-1, Moscow Region 141001, Russia, e-mail: galkin@mgul.ac.ru);
Reginald J. Hill (R/E/ET6, NOAA, US Department of Commerce, 325 Broadway, Boulder Colorado 80303, USA, e-mail: rhill@etl.noaa.gov);
Hirokazu Matsumoto (Quantum Metrology Division, National Research Laboratory of Metrology (NRLM), 1–4, Umezono 1-Chome, Tsukuba Ibaraki 305, Japan, e-mail: hiro@nrlm.go.jp);
Ruben A. Tatevian (Dept of Metrology and Standardisation, General Research Institute of Geodesy, Air-Survey and Cartography, Onezskaya 26, Moscow 125413, Russia).
3. Refractive Index of Light and Near Infrared Waves in the Atmosphere
3.1 Phase, Group, Signal and Pulse Velocity and Corresponding Refractivity
The phase refractive index (and the phase velocity) is required for the reduction of measurements with the classic Michelson interferometer and the HP (Doppler) interferometer. Traditionally, it has been assumed that electronic distance meters (EDM instruments) using amplitude, frequency or phase modulation of the carrier of flight time measurements require the group refractive index (and the group velocity). The same group refractive index is also required for the pulse distance meters used in surveying and geodesy and instruments using polarisation modulation, such a the Kern Mekometer ME 5000. (The latter is equivalent to a phase modulation as the phase of the vertical polarisation is changing against the phase of the horizontal polarisation.) White light interferometers, beat interferometers and interferometers modulated by a second wavelength also require the group index. As the next paragraph shows, the group velocity concept is an approximation that applies only if there are no absorption lines near or within the signal spectrum.
The term signal velocity was first defined by Brillouin (1960). Only recently, Oughstun et al. (1989) gave a corrected definition of signal velocity for absorptive and dispersive media. Based on Oughstun's work, Hill (in Ciddor & Hill 1999) derived the limiting conditions of the applicability of group velocity and, thus, group refractivity. Within these limits, where dispersive and absorptive distortions are negligible, the signal and the group velocities are the same. Beyond these limits, the terms group velocity and group refractive index lose their meaning because of the distortion of the wave packets. In these cases, Hill suggests to evaluate the signal velocity for specific EDM instruments using the algorithms developed by Xiao & Oughstun (1998). An alternative way accounting for the influence of resonances on (the phase and) group refractive index of air was proposed by Galkin & Tatevian (1997). A numerical comparison of the two methods has not (yet) been carried out.
The term velocity of pulse propagation is being used by Mandel & Wolf (1995, p. 822, Eq. 16.3-25). The members of the working party believe that this phenomenon likely applies to very short pulses in condensed media (with very non-linear dispersion) and to highly dispersive and/or absorbing media. The pulse velocity after Mandel & Wolf (1995) is, thus, assumed to be irrelevant to the work of the working party.
3.2 Continuum Refractivity (Dispersion)
After some lengthy discussions on the relative merits of the Edlén (1966) and the Peck & Reeder (1972) dispersion equations, preference was eventually given to Peck & Reeder. In consequence, Ciddor based his computer procedures on it (Ciddor 1996, Ciddor & Hill 1999). The advantages of the Peck & Reeder (1972) formulation are outlined in the Section on the "Two-Term Dispersion Formula" of their 1972 paper. Their arguments are convincing, particularly as the working party wants a formula that extends into the NIR. The Peck & Reeder 1972 equation differs from the Edlén 1966 equation in the following ways: (a) seven new (relative) measurements between 723 nm and 1530 nm, not used by Edlén, accuracy 1 part in 109, (b) renormalised 8 earlier data (Edlén uses initial values), (c) two earlier values (used by Edlén) omitted, (d) root mean squares of fit of 51 out of 59 data is ±1.7 ´ 10-9 whereas Edlén is ±3.1´10-9 (between 0.23 mm and 1.69 mm), (e) P&R has an average offset of 0.2 ´ 10-9 in the infrared whereas the Edlén 1966 equation has a 4.3 ´ 10-9 offset. This is clearly not acceptable for a state-of-the-art equation for geodesy.
Galkin & Tatevian indicated that they are not entirely happy with the accuracy and documentation of the original data used by Edlén and Peck & Reeder Formula. They have repeated the curve fit to the Peck & Reeder data and did not find a better solution. Galkin & Tatevian (1997a) pointed out that each absorption line in the visible and near infrared causes a small upward shift of the continuum dispersion curve towards larger wavelengths. These small increases of the refractivity with increasing wavelength cannot be modelled by the Sellmeier equations used by Peck & Reeder (and Edlén). One could add a linear term to the standard 2-3 term Sellmeier equations or add additional Sellmeier terms to the standard 2-3 term formula for resonances at about 0.7 mm, 2.5 mm and 8 mm, for example. All existing dispersion formulae could also be improved by introducing the recent absolute and relative refractivity data (e.g. data by Matsumoto, Birch & Downs, Bönsch & Potulski) and by using a better mathematical model of the curve fit that allows data sets, that were converted from relative to absolute, to float up and down as a group. Before any new curve fit one would also have to investigate the possible effect of absorption lines on old refractivity measurements.
3.3 Refractivity of Moist Air
Birch & Downs (1988a, 1988b, 1989) found an error in the original water vapour refractivity measurements of Barrell & Sears (1939). As all subsequent refractivity data were scaled to Barrell & Sears, this error is present in most existing refractivity formula. The findings by Birch & Downs were confirmed by Beers & Doiron (1992) and Bönsch & Potulski (1998). The latter confirm Birch and Downs data to within 1 part in 108. The Ciddor formulae (Ciddor 1997, Ciddor & Hill 1999) are based on Birch & Downs' new moist air refractivity data.
All new data were established at laboratory conditions. In support of outdoor measurements, new absolute measurements of water vapour refractivity over a wide range of temperatures and pressures are strongly recommended.
3.4 Lorentz-Lorenz Relationship
The limitations of the Lorentz-Lorenz relationship were referred to by Owens (1967) and by Ciddor & Hill (1999). The latter note that there is no difference in terms of "practical precision" between the Lorenz-Lorentz equation (Böttcher & Bordewijk 1978, Eq. 12.2, p. 286) and the corrected Lorenz-Lorentz equation (Böttcher & Bordewijk 1978, Eq.12.16, p.292) at atmospheric densities. The magnitude of the difference was not quantified. Ciddor believes the difference to be at the 1 part in 1012 level. According to Hill, the corrected L-L equation is only required for dense media.
Ciddor (1996) did not fully implement the Lorentz-Lorenz (L-L) relation in the new computer procedure for the refractive index of light and near infrared waves. Ciddor (1996) stated that the difference between his solution and the full LL relationship does not exceed 2 parts in 109 at an altitude of 2000 m above sea level. Later, Hill computed a difference of 5 parts in 109 for an altitude of 4500 m. Ciddor's newest computer procedure (Ciddor & Hill 1999) now includes the full (uncorrected) L-L relationship.
3.5 Anomalous Refractivity
Anomalous refractivity may be defined as the deviation from the smooth continuum dispersion curve near absorption lines. It is the contribution from anomalous dispersion by resonances to the total refractivity of air. As discussed in Section 3.1, the signal velocity after Oughstun et al. (1989) and Xiao & Oughstun (1998) will give directly the total refractivity (continuum and anomalous component) near absorption lines. The approach followed by Galkin and Tatevian (1997a, 1997b) provides only the contribution (to the total refractivity) from anomalous dispersion by resonances. Their concept is similar to the one used by Hill for infrared and radio waves (Hill et al 1980a 1980b).
According to Galkin & Tatevian (1997), the original phase refractivity data may be affected by up to 1 part in 109 due to local resonance effects. Anomalous group refractivity may reach 0.7 ppm. However, there are errors that are very much larger (several ppm!) than the published value of 0.7 ppm. Unfortunately, the magnitude of anomalous phase and group refractivity is still unknown for most wavelengths covered by the Ciddor formula. A correcting term for anomalous refractivity in Ciddor's formula is required; it could be obtained from a software package for PCs based on Galkin & Tatevian's work and suitable spectroscopic data.
Galkin & Tatevian see a certain need for a general purpose software for the computation of anomalous refractivity for wide spectrum instruments. They presently consider the following absorption lines for inclusion: N2, O2, CO2 plus water vapour. Other contenders are SO, CO, NO. They believe that CO2 and O2 can be ignored between 0.75 mm and 0.95 m and that the water absorption lines listed in HITRAN are sufficient. It would be very useful to know the magnitude of the correction and, possibly, the average correction.
3.5.1 Single Line (Laser) Instruments
As far as the visible and NIR spectrum is concerned, the modelling of anomalous phase and, in particular, group refractivity is still an open question. According to Galkin & Tatevian, very strong absorption lines can affect the phase refractive index by about one part in 10-12 to 10-13 in the visible spectrum. Near 0.77 mm, there is an effect of 1 part in 10-11 due to an oxygen line. The group refractive index is affected more by five to six orders of magnitude.
Ideally, one would like to see something like Liebe's PC-based MPM software package (e.g. Liebe 1989). As most IR instruments are not single wavelength instruments but have an (approximately) Gaussian distribution of wavelengths, the software would also have to cater for this. Investigations of anomalous group refractivity are of great interest for the following gas laser wavelengths (narrow band): 441.6 (HeCd), 632.8 nm (HeNe), 1064 nm and 532 nm (Nd:YAG). The first two are used for terrestrial dual-colour distance measurements and the latter for satellite ranging. Even though anomalous refractivity can be computed by hand, software is required if many lines are to be computed. Galkin & Tatevian do not predict a good accuracy of such computations because the (assumed) Lorenzian line shape is a model and its far-wings a problem. There is also some doubt if the AFCL HITRAN atlas lists resonances with less than 5% absorption. In the whole, Galkin and Tatevian believe that a correction for stabilised laser instruments is feasible.
3.5.2 Broadband (Diode) Instruments
Considering that, presently, about 99% of all commercial distance meters operate in the near infrared (NIR), it would be of great importance to know the effect of water vapour resonances on the group refractive index of these instruments. It is likely that the magnitude of anomalous refractivity on infrared (IR) distances meters will be reduced by the fact that they feature a Gaussian spread of the emission wavelength, usually about ±20-30 nm about the centre wavelength (at 50% power points). But this would have to be demonstrated.
Considering the 220 instrument types listed in Rüeger (1996), three popular wavelengths emerge: 820 nm, 860 nm and 910 nm. Not shown in the list are the emerging AlGaInP visible laser diodes (VLD) operating between 650 to 690 nm. It would be of great interest to know the magnitude of anomalous group refractivity at these wavelengths (670 nm, 820 nm, 860 nm, 910 nm), assuming spectral widths (at 50% power) of 3.5 nm and 40 nm for laser diodes and high radiance emitting diodes, respectively. It is known (Rüeger 1996) that the wavelengths are temperature dependent (about 0.25 to 0.35 nm/°C) and that the actual wavelength of a diode may differ by as much as 15 nm from the nominal value. So, any computations of anomalous refractivity will only be able to indicate the magnitude of the problem for diode instruments.
Galkin & Tatevian correctly point out that all depends on the number and width of the absorption lines relative to the spectral width of the EDM instrument. The effect of a narrow resonance line would be significantly reduced by a broad spectral width instrument whereas even a broad spectral width instrument would suffer greatly from anomalous refractivity if multiple absorption lines were to be distributed evenly and tightly over the spectral range of the instrument. Galkin & Tatevian note that there are more than 4000 water resonance lines between 0.75 mm and 0.95 mm.
3.6 Carbon Dioxide Content and Dispersion
A number of standard laboratories have started to use a default CO2 content of laboratory air of 400 ppm or 450 ppm. Most standard laboratories now measure the actual content and correct for it. A CO2 content of 450 ppm is clearly too high for measurements in the open (see Taylor 1994, for example). Rüeger (1998) has considered the matter and suggests 375 ppm (likely to be current in 2004) for all fixed CO2 content formulae. The proposed resolutions for simple, closed formulae are based on this assumption. The accurate formulae have an input for the actual carbon dioxide content.
The computer procedures for the accurate computation of the refractive index of air for light and near infrared waves by Ciddor (1996) and Ciddor & Hill (1999) use the Birch and Downs (1994) implementation of Edlén's (1966) CO2 correction. The deviation of the CO2 term used from that of Old et al. (1971) and Simmons (1978) is less than 1 part in 108. Even so, the Old et al.'s (1971) dispersion formula is more appropriate, as it includes the resonance effects from 4.25 mm and, thus, extrapolates much better into the infrared.
The inclusion of Old's CO2 refractivity equation in the proposed computer procedures for the accurate refractivity is of value, in particular when two-colour measurements and group refractivity are concerned. This work has begun and will be documented in the "Guidelines for the Implementation" of the Ciddor (1996) and Ciddor & Hill (1999) procedures, as foreshadowed in the proposed resolution.
3.7 Water Vapour near Saturation
The proposed simple refractivity equation and the computer procedure for a more accurate refractivity include water vapour terms. When the relative humidity increases above 70% to 90%, small water droplets may begin to form and the air may become a mixture of gases and liquid water in form of an aerosol. When operating in high humidity, it must be noted that the proposed formulae do not take account of aerosols (liquid water droplets). The resolutions cover this aspect by specifying that the formulae apply to "non-condensing "conditions only.
It might be prudent to assume the claimed accuracy of the formulae to be valid only for relative humidities below 90%. The refractive index of water (rain) in the context of electronic distance measurement (EDM) was recently investigated by Rüeger (1996b, 1999). Drizzle (1 mm/h) changes the total refractivity by about 0.03 ppm whereas heavy rain (20 mm/h) changes it by 0.3 ppm. This indicates that small quantities of liquid water will not significantly affect the continuum refractivity.
4. Resolutions on the Refractive Index of Air for Visible and NIR Waves
4.1 First Resolution
The working party has prepared two resolutions on the refractive index of air for visible and NIR waves. The first paragraph of the first resolution recommends a computer procedure for measurements to better than one part per million. The computer procedures are fully documented in Ciddor (1996) and Ciddor & Hill (1999). The Ciddor formulas produce refractivities to a few parts in 108. They match recently reported measurements within the experimental error and are expected to be reliable over very wide ranges of atmospheric conditions and wavelength. These formulas use the BIPM density equations that are valid over ranges of at least -40 to +100 °C, 800 to 1200 hPa and 0 to 100% relative humidity, and so include all practical atmospheric conditions. The formulas apply over the wavelength range from below 350 nm to above 1300 nm and, thus, cover the wavelengths at which modern surveying instruments operate. The equations take into account all known factors (except for suspended aerosols, atmospheric contaminants such as oil vapours and the effects of absorption lines) and embody the latest values of physical parameters and units.
The basic form of the phase refractive index formula used by Ciddor is as follows:
Namb = 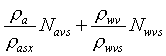 (1)
(1)
where Namb = refractivity of ambient moist air
Nasx = refractivity of dry standard air at standard conditions
(15°C, 1013.25 hPa, x ppm CO2)
Nwvs = refractivity of water vapour at standard conditions (20°C, 13.33 hPa)
rasx = density of standard air (with x ppm CO2)
rwvs = density of standard water vapour
ra = density of dry component of ambient air
rwv = density of water vapour component of ambient air
T PWVP CIDDOR OWENS EDLÉN IUGG Differences
1996 1967 1966 1963 (4-3) (5-3) (6-3)
pw NL NL NL NL
[°C] [hPa] ´10-8 ´10-8 ´10-8 ´10-8 ´10-8 ´10-8 ´10-8
(1) (2) (3) (4) (5) (6) (7) (8) (9)
l = 650 nm, CO2 content = 300 ppm (0.03%), total pressure = 1000 hPa
60 199.26 23626.92 23537.14 23413.97 23564.92 -89.78 -212.95 -62.00
45 95.85 25066.14 25018.14 24978.36 25042.27 -48.00 -87.78 -23.87
30 42.43 26484.65 26462.35 26453.76 26479.96 -22.30 -30.89 -4.69
15 17.04 27955.58 27946.75 27946.76 27957.72 -8.83 -8.82 +2.14
0 6.10 29536.31 29533.76 29533.96 29538.14 -2.55 -2.35 +1.83
-15 0.00 31283.16 31284.67 31280.87 31281.10 +1.51 -2.29 -2.06
-30 0.00 33221.68 33223.60 33215.56 33210.86 +1.92 -6.12 -10.82
l = 850 nm, CO2 content = 300 ppm (0.03%), total pressure = 1000 hPa
60 199.26 23199.45 23112.02 22986.56 23156.05 -87.43 -212.89 -43.40
45 95.85 24629.37 24582.71 24542.14 24614.12 -46.66 -87.23 -15.25
30 42.43 26032.10 26010.60 26001.80 26030.60 -21.50 -30.30 -1.50
15 17.04 27482.34 27473.94 27473.96 27485.00 -8.40 -8.38 +2.66
0 6.10 29038.32 29036.07 29036.32 29039.46 -2.25 -2.00 +1.14
-15 0.00 30756.90 30758.62 30754.88 30753.44 +1.72 -2.02 -3.46
-30 0.00 32662.81 32664.95 32657.05 32650.64 +2.14 -5.76 -12.17
Table 1: Comparison of visible and NIR group refractivity NL (in parts per 108) from the Ciddor (1996) and a number of earlier formulae. The Owens'97 data are based on Owens (1967, Eqs. (30), (31), (42); the Edlén'66 data are based on Edlén (1966, Eqs. (1) and (22), as converted from phase to group, and Eq. (12)). The IUGG'63 data follow from a subset of the equations recommended by the IUGG Resolution of 1963 (see Rüeger 1996, Eqs. (5.15) and (5.13)).
The proposed resolution refers to "Guidelines for Implementation". These will summarise the computer procedures of Ciddor (1996) and Ciddor & Hill (1999), as amended to include the Old et al. (1971) carbon dioxide dispersion formula, because of its appeal and theoretical basis in the infrared. This requires a switch from a differential correction to the computation of the total CO2 contribution, thus leading to the summation of three terms (rather than the sum of two shown in Eq. (1)), namely one each for dry air (free of carbon dioxide and water vapour), carbon dioxide and water vapour.
The second paragraph of the first resolution recommends a closed formula for measurements to not better than 1 ppm. For the latter, a subset of the equations recommended by the 1963 IUGG Resolution is being used, as amended for a value of 375 ppm for the CO2 content of the atmosphere. Table 1 shows that the chosen simple formula performs much better (at high humidity) than two formulae (OWENS'67 and EDLÉN'66) previously thought to be superior. The excellent agreement in Table 1 is due, in part, because of the use of the same values (exactly) of carbon dioxide content and partial water vapour in all formulae. Practising surveyors and geodesists will use differing equations for the saturation water vapour pressure, might omit the enhancement factor and will, typically, ignore any deviation of the actual CO2 content from the default value. For these reasons and because anomalous refractivity can amount to more than 0.7 ppm and the measurement of the atmospheric parameters can easily introduce errors of similar magnitude, the closed formula is only suggested for measurements of not better than one part per million. Please note that Table 1 is based on 300 ppm CO2 content, because all old formulae assume this content. The new formula is based on a carbon dioxide content of 375 ppm.
4.2 Second Resolution
The second resolution on the refractive index of air for visible and NIR waves suggests further work on some open questions. Firstly, the effect of absorption lines on the phase and group refractive indices of air needs to be evaluated to be able to quantify the magnitude of anomalous refractivity for specific instruments, or, in other words, the difference between the group refractivity and the signal refractivity. The numerical agreement between the approaches of Galkin & Tatevian (1997) and Oughstun (1991) should be investigated. Ideally, software should be written to evaluate the magnitude of these effects and, where possible, to correct for such effects. Such software may require better and more spectroscopic data of weak absorption lines.
As suggested earlier, it would be very useful if additional absolute and, possibly, relative measurements of the refractivity of the constituent gases of the atmosphere (including water vapour) be carried out at non-laboratory conditions, with special emphasis on near infrared wavelengths. In addition, measurements could be made in some doubtful points (for example 644 nm) of the visible spectrum.
Furthermore it should be considered to include the post-P&R data (including, in a suitable manner, relative measurements) in a revised P&R formula and to use the latter in an amended Ciddor formula. Initial steps for an amended P&R formula have been carried out by Galkin & Tatevian.
5. Refractive Index of Radio and Infrared Waves in the Atmosphere
This section is a summary of the review carried out by Rüeger (1998b) and subsequent discussions with the working group members. Refer to Rüeger (1998b) for more details.
5.1 Accuracy
Boudouris (1963) and Hartmann (1991) quoted an accuracy of the radio refractivity of 0.5% (for moist air, pw = 27 hPa) whereas Thayer (1974) claims 0.02% for dry air and 0.05% for "extremely moist air". Walter (1990 p.101, quoting Liebe 1983) states an accuracy of 0.05 ppm. As the accuracy of the radio wave refractivity is heavily dependent on the water vapour content, it is best to quote the accuracy of the dry and the wet terms separately, as done by Thayer (1974). The widely differing views on the accuracy of the water vapour refractivity may be because some authors ignore the mathematical correlation between the two water vapour terms (K2 and K3) when applying the propagation law of variances whereas others do not. (Refer to the differences between Columns 8 and 9 in Table 2 below, for example. Boudouris' (1963) accuracy estimate seems to be on the conservative side and Thayer's (1974) estimate (for the accuracy of the water vapour terms) on the optimistic side.
5.2 Continuum Formulae and Compressibility Factors
Thayer (1974, Eq. (1)) suggested a closed formula (with compressibility factors Z) of the following form:
Nr = (nr
– 1) ´
10-6 = 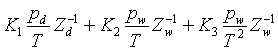 (2)
(2)
The same author noted that the omission of compressibility factors leads to errors in the radio wave refractivity of 0.04 ppm in the dry term and 0.1 ppm in the wet term at high humidities. The former is of the same magnitude as the accuracy of the dry terms whereas the latter is half of the wet term accuracy claimed by Thayer and a twentieth of the accuracy quoted by others. In consequence, it is suggested to propose a closed formula for geodesy and surveying without compressibility factors.
The International Radio Consultative Committee (CCIR) of the International Telecommunication Union (ITU), at the 16th Plenary Assembly, Dubrovnik 1986, in Recommendation 453-1, considering the necessity of using a single formula, unanimously recommended the following formula for the refractive index of radio waves:
N = (77.6/T) (P + 4810 (e/T)) (3)
with e, P in hPa, T in K. Report 563-3 gives an equivalent formula (after Bean and Dutton), with an error of less than 0.5% for frequencies of less than 100 GHz. The formula adopted by CCIR does not comprise compressibility factors and only one 'dry' term and one 'wet' term. The second (K2) term of Eq. (2) is missing.
Some authors did use compressibility factors when reducing their measured refractivities to standard conditions whereas others did not. So, one could argue that coefficients Ki that were reduced with compressibility factors can be used directly in formulae with compressibility factors. On the other hand, coefficients Ki that were determined without compressibility factors can be used directly in formulae without compressibility factors. Considering Eq. (2), it becomes clear that the coefficients Ki in formulae without compressibility factors really cannot be numerically the same as those in formulae with compressibility factors. This aspect must yet be verified in all known formulae of interest in this context.
It might be desirable that precision formulae use compressibility factors Zi and the matching Ki constants for dry (carbon dioxide free) air, water vapour and carbon dioxide terms even though the compressibilities change refractivity by less than the claimed accuracy of the formulae. To be consistent with the recommended formulae for the visible and NIR waves, the compressibility factors should be computed with the BIPM formulae. See Ciddor (1996) for reference.
5.3 Carbon Dioxide
Following the recommendations in the proposed resolutions on the refractivity of light and near infrared waves, it is again suggested to use a 375 ppm fixed CO2 content in all new closed formulae, like those for hand calculations. This has been implemented in Eq. (6) (Rüeger 1998b). The change from 300 to 375 ppm changes the radio wave refractivity by only 0.01 ppm at standard conditions. To be consistent, it is suggested that precise formulae and models should include the CO2 content as input variable. A default of 375 ppm CO2 could be implemented in MPM as well as an optional CO2 content input.
5.4 Upper Frequency Limit for Closed Refractivity Formula
Different authors quote different upper limits for the non-dispersive region of radio wave refractivity. For example, Hartmann (1991) quoted 5 GHz, Thayer (1974) 20 GHz and Boudouris (1963) 30 GHz. These limits vary because of the magnitude of spurious effects tolerated and the accuracy of formulae assumed by these authors. Rüeger (1998b) suggested 1 GHz as cut-off as Liebe (1996) suggests additional terms for dispersive refractivity above 1 GHz. This limit is sufficiently removed from the nearest resonance frequencies of water vapour and oxygen. Liebe (1983) and Hartmann (1991) list, for example, H2O resonances at 22.23 GHz, 67.81 GHz, 119.99 GHz, 321.22 GHz, and O2 resonances between 53.59 GHz and 66.30 GHz and at 118.75 GHz. Further evaluation of the magnitude of the effect of absorption lines might permit to extend the validity range of simple closed formulae to 5 GHz or 10 GHz.
5.5 Dispersive Refractivity (to 1 THz)
As Hill et al. (1980) and Liebe (1989) did, dispersive refractivity can be added to experimental refractivity. Liebe's Millimetre-Wave Propagation Model (MPM) is the only operational model to account for 44 oxygen and 30 local water resonance lines plus an empirical water vapour continuum to offset experimental discrepancies. The CO2 resonance at 15 mm should be sufficiently distant to cause anomalous refractivity between 1 Hz and 1THz.
5.6 Phase, Group and Signal Velocity
In geodesy and surveying, it has been generally assumed that the refractive index of radio waves is not dependent on the carrier frequency and, thus, only the phase refractive index must be considered. Microwave electronic distance measurements (EDM) used frequency modulation techniques to derive the distance measurements. GPS signals are code modulated but reconstructed carrier waves are usually used for the actual measurement in geodesy. It could be argued that, since some of the radio wave spectrum is dispersive, the concept of group or signal refractivity might have to be introduced where the propagation of modulated waves is used for measurements. If the visible spectrum can be taken as a guide then the anomalous group refractivity can be 100'000 times larger than the anomalous phase refractivity.
The question now arises if the concept of group velocity or signal velocity has to be introduced in the dispersive regions of the radio wave spectrum. According to Hufford, "signal velocity" is already used for the wave propagation in wave guides. Hufford (1987) did compute the millimetre-wave pulse distortion by a single absorption line simulating the terrestrial atmosphere and, therein, gives a reference to Trizna & Weber (1982), which also discuss the signal velocity for pulse propagation in a medium with resonant anomalous dispersion.
Further investigation and quantification of the difference between phase and signal velocity in the frequency ranges 1 Hz to 1 GHz (non-dispersive) and 1 GHz to 1THz (dispersive) are clearly required.
5.7 Anomalous Refractivity Effect in Historic Data
Most radio wave refractivity data were measured above 1 GHz, were dispersive refractivity starts to have an effect. For example: Birnbaum & Chatterjee (1952; 9.28 GHz, 24.8 GHz), Boudouris (1963; 7 GHz to 12 GHz), Newell & Baird (1965; 47.7 GHz), Liebe (1969; 22.235 GHz), Liebe et al (1977; 53.5 to 63.5 GHz). The last two determinations accounted for anomalous refractivity whereas the first three did not.
To get consistent data for the derivation of a dispersion-free radio wave refractivity, it would be of great benefit if anomalous refractivity were removed from experimental data. In particular, it would be worthwhile to remove anomalous refractivity from the values in Newell & Baird's Table III (1965) for dry air and oxygen. The poor agreement of Froome's oxygen value could be entirely due to dispersive oxygen refractivity.
6. Refractivity for IR and Radio Waves: Work to Date and Pending Work
6.1 Formula for Hand Calculations (1 Hz to about 1 GHz, ¥ m to 0.3 m)
It is valuable to have a relative simple and closed solution for the refractive index of radio waves for easy calculation with pocket calculators and personal computers. The equations given here are empirical, based on experiment and ignore the non-ideal gas behaviour (compressibility) of air.
When ignoring compressibility factors, the refractivity Nr of radio waves (in ppm) can be expressed as:
Nr = ( nr
– 1 ) ´
106 = 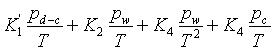 (4)
(4)
where pd-c (= pd – pc = ptot - pw – pc) is the (partial) pressure of the dry and carbon-dioxide-free air, pd is the (partial) pressure of the dry air ( = ptot - pw), pw is the partial water vapour pressure, pc is the partial carbon dioxide pressure, the Ki are constants and T the temperature (in K). The coefficient K is the constant K1 without the CO2 component. Because of its polar nature, water vapour has a density and a density-temperature term.
Based on the coefficients by Boudouris (1963: K2 and K3) and Newell & Baird (1965: K1 and K4) Rüeger (1998b) constructed a three-term equation for air with 0.03% (300 ppm) CO2 content:
Nr = ( nr
– 1 ) ´
106 = 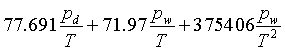
where the dry air (including carbon dioxide) pressure pd (= ptot - pw) and the partial water vapour pressure pw are taken in hPa and the temperature T in K. The accuracy of an equivalent equation is estimated by Boudouris (1963, p. 661) to be within 0.5% for temperatures between -50°C and +40°C, (total) pressures between 187 and 1013.25 hPa, partial water vapour pressures between 0 and 27 hPa and frequencies between 1 Hz and 30 GHz.
Recomputing the K1 term for the carbon dioxide content of 375 ppm (0.0375%), expected to be current around the year 2004, gives the final form of a possible new formula for the non-dispersive radio wave refractivity Nr (after Boudouris-Newell-Baird, in units of K and hPa)
Nr = ( nr
– 1 ) ´
106 = 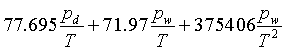 (6)
(6)
A comparison of this equation with other formulae can be found in Table 2.
6.2 Computer Routine (1 Hz to about 1 THz, ¥ m to 0.3 mm)
A practical model that simulates the complex refractive index for the propagation calculation of electromagnetic waves through the atmosphere has been developed by Liebe et al. over many years. The Millimetre-Wave Propagation Model (MPM) is as a program for frequencies below 1000 GHz in the atmosphere running on personal (IBM compatible) computers. The MPM "consists of 44 oxygen and 30 local water resonance lines, of non-resonant spectra for dry air and of an empirical water vapour continuum that reconciles experimental discrepancies" (Liebe et al. 1992). The model is applicable for barometric pressures between 0 and 1200 hPa, ambient temperatures between -100 and +50°C, relative humidity between 0 and 100% and suspended water droplets and ice particle densities between 0 and >5 g/m3. (Other versions of MPM also model rainfall conditions.) The complete (complex) refractivity model is as follows (Liebe et al. 1992, Liebe et al. 1993, Liebe 1996):
N = ND + NV + NW,I (7)
where the complex dry-air refractivity is denoted by ND, the refractivity of atmospheric water vapour by NV and the complex refractivity of suspended water droplets and ice particles by NW,I . Complex parameters are shown in bold type. Only the real-part is required for the computation of the refractivity. The refractivity of suspended water droplets and ice particles (for example in fog and in clouds) is of no direct interest in this context. The complex dry-air refractivity ND is computed (in ppm) from (Liebe et al. 1992, Liebe 1996)
ND = Nd + SkSkFk + SoFo + i SnF (8)
where Nd is the non-dispersive (dry-air) term, k is the index of the 44 oxygen resonances, Sk is the line strength and Fk the complex spectral shape function. So and Fo model the non-resonant refractivity below 10 GHz from the oxygen relaxation spectrum. The SnF term models the pressure-induced nitrogen absorption above 100 GHz. The MPM computes the refractivity of atmospheric water vapour NV (in ppm) as follows (Liebe et al. 1992, Liebe et al. 1993, Liebe 1996):
NV = Nv + SlSlFl + SoFo + NC (9)
where Nv is the non-dispersive water vapour refractivity, l is the index of the 30 local water resonances, Sl is the line strength and Fl the shape function. The continuum refractivity NC models contributions over and above the 30 local lines and is partly based on the work by Hill (1988).
The MPM makes use of spectral data and is supported by many laboratory measurements to validate and enhance the overall performance of the model. The authors note that MPM dry-air absorption values agree with measured ones at the 1% level. "Model predictions involving water vapour and water droplets are estimated to lie in the 10 per cent range" (Liebe et al. 1992). MPM does not consider the weak spectra of trace gases such as O3, CO and N2O nor does it provide an input for the CO2 content. Presumably, a carbon dioxide content of 0.03% is assumed and included in the dry-air non-dispersive term.
6.3 Comparison of Formulae
Table 2 shows a comparison of the Millimetre-Wave Propagation Model (MPM, non-dispersive refractivity (Nd) only) with the simple formulae by Essen & Froome (1951), Boudouris (1963), a formula based on Liebe's (1977) coefficients and the B-N-B formula developed above (Eqs. (5) and (6), after Boudouris (1963) and Newell & Baird (1965)). At a later stage, it might be of interest to compare Eq. (3) adopted by the International Telecommunications Union.
A total pressure (ptot) of 1000 hPa exactly was used for the comparison. To be consistent with the historical equations, the B-N-B formula for a CO2 content of 0.03% (300 ppm) was used (Eq. (5) rather than Eq. (6)). The relative humidity was set at 100% for temperatures between 0°C and 60°C. The saturation water vapour pressures used for the computations of Columns 4, 5, 6 and 7 are shown in Column 2 and were taken from Rüeger (1990, 1996, Appendix B, after Goff & Gratch 1946). MPM uses relative humidity as input and converts it to partial water vapour pressure using Goff & Gratch (1946). The precision of the new B-N-B formula (Eq. (6)) was predicted using the propagation law of variances and the given precisions of the constants K1, K2 and K3. Column 8 gives the precision without consideration of the correlation between the constants K2 and K3. Column (9) uses a correlation coefficient of 0.995 between the two constants to compute the covariance between them. (The correlation coefficient was obtained from a repeat of Boudouris' curve fit.)
T PWVP MPM93 E&F51 Liebe77 Boud63 B-N-B Prec Prec (4-3)
(5-3) (6-3) (7-3)
pw Nr Nr Nr Nr Nr B-N-B B-N-B
[°C] [hPa] ´10-6 ´10-6 ´10-6 ´10-6 ´10-6 ´10-6 ´10-6 ´10-6 ´10-6 ´10-6 ´10-6
(1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13)
± ±
60 199.26 902.2 892.9 902.2 903.5 903.7 8.3 1.2 -9.2 0.0 1.4
1.6
45 95.85 597.1 592.3 597.1 597.7 598.0 4.2 0.5 -4.8 0.0 0.6
0.9
30 42.43 428.3 426.0 428.4 428.5 428.8 2.0 0.2 -2.3 0.1 0.2
0.5
15 17.04 346.0 345.0 346.1 346.0 346.3 0.9 0.1 -1.0 0.1 0.0
0.3
0 6.10 314.8 314.3 314.9 314.6 315.0 0.3 0.0 -0.5 0.1 -0.1 0.2
-15 0.00 300.8 300.7 300.9 300.6 301.0 0.0 0.0 -0.1 0.1 -0.2
0.2
30 0.00 319.3 319.2 319.5 319.1 319.5 0.0 0.0 -0.1 0.0 -0.2
0.2
Table 2: Comparison of the non-dispersive part of the radio wave refractivity Nr (in parts in per million) from the Millimetre-Wave Propagation Model (MPM'93) and a number of simple formulae.
Table 2 shows clearly that the Essen & Froome equation (1951), adopted by IUGG in 1963, differs significantly from the other three models at high temperature and humidity. The Essen & Froome formula agrees better than any other with Liebe's MPM below freezing point and at zero humidity. The water vapour refractivity used by Essen & Froome is not optimal. Not unexpectedly, the formula ("Liebe77") based on the K1, K2 and K3 terms by Liebe et al. (1977b) agrees very well with the MPM. The differences in Column 11 of Table 2 do not exceed 0.15 ppm between -30°C and +60°C. Boudouris' formula agrees slightly better with the MPM than the Boudouris-Newell-Baird formula derived above. The B-N-B formula gives values that are, on average, 0.3 ppm higher than those of Boudouris. This is expected as Newell & Baird's K1 constant is slightly larger than that of Boudouris and as the B-N-B formula (Column 7) uses the same K2 and K3 constants as Boudouris (Column 6). It is also evident that the Boudouris and the B-N-B formulae have offsets from the MPM of the same magnitude but of different sign at negative temperatures and zero humidity. The differences (6)-(3) and (7)-(3) compare better with the precision values in Column (9), which take account of the (mathematical) correlation between K2 and K3, than with those in Column (8), which don't. It follows that the correlation between K2 and K3 should not be ignored when predicting the precision of computed refractivity.
It follows from Table 2 that it might be appropriate the Liebe 1977 formula if MPM'93 were to be adopted for precision measurements in geodesy. On the other hand, if the new B-N-B formula of Eq. (6) were adopted as a simple equation, then it might be necessary to change MPM and REFRAC-IAG (see below) accordingly.
6.4 Proposal for REFRAC-IAG
The Millimetre-Wave Propagation Model (MPM) of the (US) National Telecommunications and Information Administration (NTIA) in Boulder presently best meets the IAG requirements for a computer procedure for the computation of the phase refractive index of radio and millimetre waves. Mr. M. Cotton of NTIA/ITS has started work for an IAG version of the MPM derivative program REFRAC, provisionally named REFRAC-IAG. Some changes to MPM suggested by Hill (1988, Eq.9, Table II) have already been implemented. Work for the input of a variable CO2 content has begun. It will be based on K4 = 133.5 ±0.15 (K/hPa)and used a default content of 375 ppm. The user interface of REFRAC-IAG has been changed from that of REFRAC to simplify the use of the program.
Further questions to be addressed are that of using the BIPM saturation water vapour pressure formula (and enhancement factor) as used in Ciddor (1996) and Ciddor & Hill (1999), the sources and history of Liebe's K1, K2 and K3 terms and the question of the suitability or necessity of compressibility factors. It is possible, that an introduction of compressibility factors into MPM and REFRAC-IAG could compromise the integrity of the package.
7. Resolutions on the Refractive Index of Air for Radio and NIR Waves
The third resolution proposed for adoption at the 22nd General Assembly of IUGG notes that the radio refractive index formula (after Essen & Froome) recommended in Resolution No. 1 of the 13th General Assembly of IUGG (Berkley 1963) is now clearly out of date, as the Column 10 in Table 2 shows. With new absolute and relative measurements of the mid-infrared to radio wave refractive index of air and considerable advances having been made with the computation of anomalous refractivity in the mid-infrared to radio wave spectrum, there is a clear need to amend the 1963 IUGG resolutions.
Although some progress has been made towards new recommendations for a simple closed formula and a more accurate computer procedure, more work is clearly required. Sections 5 and 6 indicate the progress made and the open questions that remain. In particular, the need for compressibility factors needs to be investigated and the significance of the difference between the signal velocity and the phase velocity in geodetic measurements through the atmosphere established. The ad hoc working party is looking for interested scientists that are able to contribute to this work on a new recommendation for the mid-infrared to radio (phase and signal) refractive index in air. Depending on the choice of a best possible simple formula, the coefficients K1, K2 and K3 used by MPM and REFRAC-IAG might have to be adjusted.
8. Outlook
The ad-hoc working party considers its work on the continuum refractive index of visible and near infrared waves completed. Some possible improvements to the dispersion equation have been indicated all the same. From now onwards, the ad-hoc working party proposes to concentrate on the effects of absorption lines in the visible and near infrared regions of the spectrum on one hand and on the radio refractive index on the other. It is hoped that resolutions on the remaining aspects can be formulated well before the next General Assembly. Experts, particularly in the field of radio wave refractivity, that are able to contribute to the work are invited to join the group.
9. Bibliography and Literature
Balsamo, A., Zangirolami, M. 1995. An Absolute Refractometer for Precise Length Measurement. Proc., Int Precision Engineering Seminar (IPES'95), Compiège, France, 93-96.
Barrell, H., Sears, J. E. 1939. The Refraction and Dispersion of Air for the Visible Spectrum. Philos. Trans. R. Soc. London, Ser. A 238: 1-64.
Bechler, A. 1999. Quantum Electrodynamics of the Dispersive Dielectric Medium – A Path Integral Approach. J. Modern Optics, 46(5), 901-921.
Beers, J., Doiron, T. 1992. Verification of Revised Water Vapour Correction to the Index of Refraction of Air. Metrologia, 28: 315-316.
Birch, K. P. 1991. Precise Determination of Refractometric Parameters for Atmospheric Gases, J. Opt. Soc. Am. A, 8(4):647-651.
Birch, K. P., Downs, M. J. 1994. Corrections to the Updated Edlén Equation for the Refractive Index of Air. Metrologia, 31:315-316.
Birch, K. P., Downs, M. J. 1993. An Updated Edlén's Equation for the Refractive Index of Air. Metrologia, 30:155-162.
Birch, K. P., Downs, M. J. 1989. Error Sources in the Determination of the Refractive Index of Air. Applied Optics, 28(5): 825-826.
Birch, K. P., Downs, M. J. 1988a. The Precise Determination of the Refractive Index of Air, National Physical Laboratory, NPL Report MOM90, July 1988, 35 pages.
Birch, K. P., Downs, M. J. 1988b. The Results of a Comparison Between Calculated and Measured Values of the Refractive Index of Air. J. Phys. E: Sci. Instrum., 21: 694-695.
Birch, K. P., Reinboth, F., Ward, R. E., Wilkening, G. 1993. The Effect of Variations in the Refractive Index of Industrial Air upon the Uncertainty of Precision Length Measurement. Metrologia, 30: 7-14.
Birnbaum, G., Chatterjee, S. K. 1952. The Dielectric Constant of Water Vapour in the Microwave Region. J. App. Phys., 23: 220-223.
Bönsch, G. Potulski, E. 1998a. Measurement of the Refractive Index of Air and Comparison with Modified Edlén's Formulae. Metrologia, 35: 133-139.
Bönsch, G., Potulski, E. 1998b. Fit of Edlén's Formulae to Measured Values of the Refractive Index of Air. Proc. Recent Developments in Optical Gauge Block Metrology. 20-12 July 1999, San Diego, USA, Vol. 3477, SPIE Proceedings Series, 0277-786X/98, 62-67.
Böttcher, C. J. F. 1952. Theory of Electric Polarisation. Elsevier, Amsterdam.
Böttcher, C. J. F. 1973. Theory of Electric Polarisation. 2nd ed., Vol. I, Elsevier, Amsterdam.
Böttcher, C. J. F., Bordewijk, P. 1978. Theory of Electric Polarisation. 2nd ed., Vol. II, Elsevier, Amsterdam.
Born, M., Wolf, E. 1980. Principles of Optics. 6th ed., Pergamon, Oxford, UK.
Boudouris, G. 1963. On the Index of Refraction of Air, the Absorption and Dispersion of Centimetre Waves by Gases. J. of Res. of the Nat. Bureau of Standards – D. Radio Propagation, 67D(6): 631–684.
Brillouin, L. 1960. Wave Propagation and Group Velocity. Academic Press, New York.
Ciddor, P. E., Hill, R. J. 1999. Refractive Index of Air. 2. Group Index. Applied Optics (Lasers, Photonics and Environmental Optics), 38(9): 1663-1667.
Ciddor, P. E. 1996. Refractive Index of Air: New Equations for the Visible and Near Infrared. Applied Optics (Lasers, Photonics and Environmental Optics), 35(9): 1566-1573.
Cuthbertson, C., Cuthbertson, M. 1920. On the Refraction and Dispersion of Carbon Dioxide, Carbon Monoxide and Methane. Proc. R. Soc. London, Ser.A 97: 152-159.
Davies, R. S. 1992. Equation for the Determination of the Density of Moist Air (1981/91). Metrologia, 29:67-90
Deichl, K. 1984. Der Brechungsindex für Licht- und Mikrowellen. Allgemeine Vermessungsnachrichten (AVN), 91:85-100.
Edge, R. C. A. 1960. Report of IAG Special Study Group No.19 on Electronic Distance Measurement using Ground Instruments. Presented at 12th General Assembly of IUGG, Helsinki, 1960.
Edlén, B. 1966. The Refractive Index of Air. Metrologia, 2(2): 12-80.
Edlén, B. 1953. The Dispersion of Standard Air. J. Opt. Soc. Am, 43: 339-344.
Erickson, K. E. 1962. Investigation of the Invariance of Atmospheric Dispersion with a Long-Path Refractometer. J. Opt. Soc. of America, 52(7):777-780.
Earnshaw, K. B., Owens, J. C. 1967. A Dual-Wavelength Optical Distance Measuring Instrument which Corrects for Air Density. IEEE J. Quantum Electron., QE-3: 544-550.
Essen, L., Froome, K. D. 1951. The refractive indices and dielectric constants of air and its principal Constituents at 24 GHz. Proc Phys Soc (London) B-64:862-875.
Galkin, Y. S., Tatevian, R. A. 1997a. The Problem of Obtaining Formulae for the Refractive Index of Air for High-Precision EDM. Journal of Geodesy, 71:483-485.
Galkin, Y. S., Tatevian, R. A. 1997b. Influence of Resonances on the Phase and Group Refractive Indices of Air. Journal of Geodesy, 71:680-684.
Genike, A. A., Galkin, Y. S. 1975. The Effect of Molecular Resonances on the Group Velocity of Light in Electromagnetic Distance Measurement. Presented at the 16th General Assembly of IUGG, Grenoble, France, August 1997, 14 pages.
Giacomo, P. 1982. Equation for the Determination of the Density of Moist Air. Metrologia, 18:33-40.
Gobulev, A. N. 1985. On the Problem of the Velocity of Light Determination in Optical Distance Measurement. Proc., Institute of Higher Education Series Geodesy and Aerial Surveying, USSR, No. 5, 20-29 (in Russian)
Goff, J. A., Gratch, S. 1946. Low Pressure Properties of Water from -160 to 212°F. Transactions, American Society of Heating and Ventilating Engineers, 52:95-122.
Guzzi, R., Rizzi, R. Water Vapour Absorption in the Visible and Near-Infrared: Results of Field Measurements. Applied Optics, 23(11): 1853-1861.
Hartmann, G. K. 1991. The Determination of Tropospheric Conditions (Especially H2O) Affecting the Accuracy of Position Measurements. Paper presented at 20th General Assembly, IUGG, Vienna, 23 August 1991, (Symposium on Environmental Effects on Spacecraft Trajectories and Positioning), 28 pages.
Hartmann, G. K., Leitinger, R. 1984. Range Errors due to Ionospheric and Tropospheric Effects for Signal Frequencies above 100 MHz. Bulletin Géodésique, 58: 109-136.
Heimann, M. 1996. Closing the Atmospheric CO2 Budget: Inferences from new Measurements of 13C/12C and O2/N2 Ratios. Global Change (IGBP) Newsletter, 28: 9-11.
Hill, R. J. 1996. Refractive Index of Atmospheric Gases. Chapter II.3.1.1 in: Dieminger-Hartmann-Leitinger (eds), The Upper Atmosphere, Springer-Verlag, Berlin-Heidelberg-New York, 261-270.
Hill, R. J. 1988. Dispersion by Atmospheric Water Vapour at Frequencies less than 1 THz. IEEE Trans. on Antennas and Propagation, 36(3): 423-430.
Hill, R. J., Lawrence, R. S. 1986. Refractive Index of Water Vapour in Infrared Windows. Infrared Physics, 26(6): 371-376.
Hill, R. J., Lawrence, R. S., Priestley, J. T. 1982. Theoretical and Calculational Aspects of the Radio Refractive Index of Water Vapour. Radio Science, 17(5): 1251-1257.
Hill, R. J., Clifford, S. F. 1981. Contributions of Water Vapour Monomer Resonances to Fluctuations of Refraction and Absorption for Submillimetre Through Centimetre Wavelengths. Radio Science, 16(1):77-82.
Hill, R. J., Clifford, S. F., Lawrence, R. S. 1980a. Refractive Index and Adsorption Fluctuations in the Infrared caused by Temperature, Humidity and Pressure Fluctuations, J. Opt. Soc. Am., 70(10): 1192-1205.
Hill, R. J., Clifford, S. F., Lawrence, R. S. 1980b. Computed Refraction and Absorption Fluctuations caused by Temperature, Humidity and Pressure Fluctuations – Radio Waves to 5 mm. NOAA Technical Memorandum, Environmental Research Laboratories, Wave Propagation Laboratory, ERL WPL-59, 64 pages.
Hinderling, J., Sigrist, M. W., Kneubühl, F. K. 1987. Laser-Photoacoustic Spectroscopy of Water-Vapour Continuum and Line Absorption in the 8 to 18 mm Atmospheric Window. Infrared Physics, 27(2): 63-120.
Hou, W., Thalmann, R. 1994. Accurate Measurement of the Refractive Index of Air. Measurement, 14: 307-314.
Hufford, G. 1987. Millimetre-Wave Pulse Distortion by a Single Absorption Line Simulating the Terrestrial Atmosphere. NTIA Report 87-229, National Telecommunications and Information Administration (NTIA), 325 Broadway, Boulder CO 80303, 39 pages.
Hyland, R. W., Wexler, A. Formulations for the Thermodynamic Properties of the Saturated Phases of H2O from 173.15 K to 473.15 K. ASHRAE Trans., 89: 500-511.
IUGG (International Union of Geodesy and Geophysics). 1963. Resolutions, 13th General Assembly, 19-31 August 1963, Berkeley, California, USA. Bulletin Géodésique, 70:390.
Jansco, G., Pupezin, J., Van Hook, W. A. 1970. The Vapour Pressure of Ice between +10+2 and -10+2. J. Phys. Chem., 74: 2984-2989.
Jones, F. E. 1981. The Refractivity of Air. J. Res. Natl. Bur. Stand., 86: 27-32.
Jones, F. E. 1980. Simplified Equation for Calculating the Refractivity of Air. Appl. Opt., 19: 4129-4130.
Langley, R. B. 1992. The Effect of the Ionosphere and Troposphere on Satellite Positioning Systems. Abstract in: DeMunck, J. C. & Spoelstra, T. A. T. (eds.) Proc., Symposium on Refraction of Transatmospheric Signals in Geodesy, 19-22 May 1992, The Hague, Netherlands Geodetic Commission, Publications on Geodesy, New Series, No.36, p. 97 (full paper 10 pages).
Leitinger, R. 1996. Transatmospheric Propagation of Radio Waves: The Role of the Atmosphere in Communication, Navigation, Geodesy etc. Chapter I.7 in: Dieminger - Hartmann, Leitinger (Eds.), The Upper Atmosphere – Data Analysis and Interpretation, Springer-Verlag, Berlin-Heidelberg-New York, 169-187.
Liebe, H. J. 1996. Models for the Refractive Index of the Neutral Atmosphere at Frequencies Below 1000 GHz. Chapter II.3.1.2 in: Dieminger-Hartmann-Leitinger (eds.), The Upper Atmosphere – Data Analysis and Interpretation. Springer-Verlag, Berlin-Heidelberg-New York, 1996, 270-287.
Liebe, H. J. 1989. MPM – An Atmospheric Millimetre Wave Propagation Model. Int. Journ. Infrared and Millimetre Waves, 10(6): 631-650.
Liebe, H. J. 1983. An Atmospheric Millimetre Wave Propagation Model. NTIA Report 83-137, National Telecommunications and Information Administration (NTIA), 325 Broadway, Boulder CO 80303, 110 pages.
Liebe, H. J. 1969. Calculated Tropospheric Dispersion and Absorption due to the 22 GHz Water Vapour Line. IEEE Transactions on Antennas and Propagation, AL-17(5): 621-627.
Liebe, H. J. 1966. Über Untersuchungen des Brechungsindex von Wasserdampf-Stickstoff im Bereich 3 bis 14 GHz. Nachr. Techn. Z., 19:79-83.
Liebe, H. J., Hufford, G. A., Cotton, M. G. 1993. Propagation Modeling of Moist Air and Suspended Water/Ice Particles at Frequencies below 1000 GHz. AGARD, 52nd Specialists' Meeting of the Electromagnetic Wave Propagation Panel, Palma da Mallorca, Spain, 17-21 May 1993, 3-1 to 3-10.
Liebe, H. J., Hufford, G. A., Cotton, M. G. 1992. Progress in Atmospheric Propagation Modelling at Frequencies below 1000 GHz. Proc., 1992 Battlefield Atmospherics Conference, 1-3 December 1992, Fort Bliss, El Paso, Texas, 247-256.
Liebe, H. J., Hufford, G., Manabe, T. 1991. A Model for the Complex Permittivity of Water at Frequencies below 1 THz. Int. Journ. Infrared and Millimetre Waves, 12(7): 659-675.
Liebe, H. J., G. A. Hufford, R. O. DeBolt. 1991. The Atmospheric 60-GHz Oxygen Spectrum: Modelling and Laboratory Measurements. NTIA Report 91-272, National Telecommunications and Information Administration (NTIA), 325 Broadway, Boulder CO 80303, 36 + 124 pages.
Liebe, H. J., D. H. Layton. 1987. Millimetre-Wave Properties of the Atmosphere: Laboratory Studies and Propagation Modelling. NTIA Report 87-224, National Telecommunications and Information Administration (NTIA), 325 Broadway, Boulder CO 80303, 74 pages.
Liebe, H. J., Hopponen, J. D. 1977a. Variability of EHF air Refractivity with Respect to Temperature, Pressure and Frequency. IEEE Trans. on Antennas and Propagation, AP-25(3): 336-345.
Liebe, H. J., Gimmestad, G. G., Hopponen, J. D. 1977b. Atmospheric Oxygen Microwave Spectrum – Experiment versus Theory. IEEE Trans. on Antennas and Propagation, AP-26(3): 327-335.
McCoy, J. H., Rensch, D. B., Long, R. K. 1969. Water Vapour Continuum Absorption of Carbon Dioxide Laser Radiation near 10 mm. Applied Optics, 8(7):1471-1478.
Mandel, L., Wolf, E. 1995. Optical Coherence and Quantum Physics. Cambridge University Press, UK.
Marti, J., Mauersberger, K. 1993. A Survey and New Measurements of Ice Vapour Pressure at Temperatures between 170 K and 250 K. Geophys. Res. Lett., 20: 363-366.
Matsumoto, H. 1987. The Refractivity of CO2 Gas in the Region of 10 mm. Applied Physics B, 44:147-149.
Matsumoto, H. 1984. The Refractivities of Water Vapour for CO2 Laser Lines. Optics Communications, 50(6): 356-358.
Matsumoto, H. 1982a. Measurement of the Group Refractive Index of Air by Two-Wavelength Interferometry. Optics Communications, 44(1): 5-7.
Matsumoto, H. 1982b. The Refractive Index of Moist Air in the 3 mm Region. Metrologia, 18:49-52.
Matsumoto, H., Zeng, L. 1994. High-Accuracy Measurement of Air Refractive Index using two Frequency-Doubling Crystals. Optics Communications 104:241-244
Matsumoto, H., Kurosawa, T., Iwasaki, S. 1988. Verification of the Accuracy of a CO2 Laser Interferometer for Distance Measurement. Metrologia, 25:95-97.
Mendes, V. B. 1999. Modelling the Neutral-Atmosphere Propagation Delay in Radiometric Space Techniques. PhD dissertation, Department of Geodesy and Geomatics Engineering Technical Report No. 199, University of New Brunswick, Fredericton, New Brunswick, Canada, 353 pages.
Mujlwijk, R. 1988. Update of the Edlén Formulae for the refractive Index of Air. Metrologia, 25: 189. C. Rischel and P. S. Ramanujam, Refractive Index of Air – Errata, Metrologia, 26: 263 (1989).
NASA. 1987. From Pattern to Process: The Strategy of the Earth Observing System – EOS Science Steering Committee Report, Vol. II, 140 pages.
Newell, A. C., Baird, R. C. 1965. Absolute Determination of Refractive Indices of Gases at 47.7 GHz. Journal of Applied Physics, 36(12): 3751-3759.
Old, J. G., Gentili, K. L., Peck, E. R. 1971. Dispersion of Carbon Dioxide. J. Opt. Soc. Of America, 61(1): 89-90.
Oughstun, K. E. 1991. Pulse Propagation in a linear, causally dispersive Medium. Proc. IEEE, 79(10), 1370-1390.
Oughstun, K. E., Wyns, P., Foty, D. 1989. Numerical Determination of the Signal Velocity in Dispersive Pulse Propagation. J. Opt. Soc. Am., A 6, 1430-1440.
Owens, J. C. 1967. Optical Refractive Index of Air: Dependence on Pressure, Temperature and Composition. Applied Optics, 6(1): 51-59.
Peck, E. R. 1986. Precise Measurements of Optical Dispersion using a new Interferometric Technique: Comment. Appl. Opt., 25: 3597-3598.
Peck, E. R., Reeder, K. 1972. Dispersion of Air. Journal of the Optical Society of America, 62(8): 958-962.
Peck, E. R., Khanna, B. N. 1962. Dispersion of Air in the Near-Infrared. Journal of the Optical Society of America, 52(4): 416-419
Preston-Thomas, H. 1990. The International Temperature Scale of 1990 (ITS-90). Metrologia, 27:3-10
Rothman, L. S., Schroeder, J., McCann, A., Gamache, R. R., Wattson, R. B., Flaud, J.-M., Perrin, A., Dana, V., Mandin, J.-Y., Goldman, A., Massie, S., Varassi, P., Yoshino, K. The 1996 HITRAN Molecular Spectroscopic Database and HAWKS (HITRAN Atmospheric Workstation), submitted to Journal of Quantitative Spectroscopy and Radiative Transfer.
Rothman, L. S., Gamache, R. R., Tipping, R. H., Rinsland, C. P., Smith, M. A. H., Chris Benner, D., Malathy Devi, V., Flaud, J.-M., Camy-Peyret, C., Perrin, A., Goldman, A., Massie, S. T., Brown, L. R., Toth, R. A. 1992. The HITRAN Molecular Database: Editions of 1991 and 1992. J. Quant. Spectrosc. Radiat. Transfer, 48(5/6): 469-507.
Rüeger, J. M. 1999. Refractive Index of Water and Electro-Optical Distance Measurement through Rain. Survey Review, 35(271): 11-22.
Rüeger, J. M. 1998a. Refractive Index Formulae for Electro-Optical Distance Measurement. Proc., Commission 5, 21st International Congress (FIG'98), International Federation of Surveyors, 19-25 July 1998, Brighton, UK, 191-208.
Rüeger, J. M. 1998b. Refractive Index Formulae for Electronic Distance Measurement with Radio and Millimetre Waves, 13 pages (in Preparation).
Rüeger, J. M. 1996a. Electronic Distance Measurement – An Introduction. 4th ed. Springer-Verlag, Berlin-Heidelberg-New York, 276 + xix pages.
Rüeger, J. M. 1996b. Einfluss von Regen auf die elektronische Entfernungsmessung, XII. Int. Kurs für Ingenieurvermessung, Graz, 9-14 September 1996, in: Brandstätter/Brunner/Schelling (Eds.), Ingenieurvermessung 96, Vol. 1, Dümmler, Bonn, 1996, A10/1 - A10/10.
Rüeger, J. M. 1990. Electronic Distance Measurement – An Introduction. 3rd ed. Springer-Verlag, Berlin-Heidelberg-New York, 266 + xvii pages.
Schellekens, P., Wilkening, G., Rinboth, F., Downs, M. J., Birch, K. P., Spronck, J. 1986. Measurements of the Refractive Index of Air using Interference Refractometers. Metrologia, 22: 279-287.
Schiebener, P., Straub, J., Levelt Sengers, J. M. H., Gallagher, J. S. 1990. Refractive Index of Water and Steam as Function of Wavelength, Temperature and Density. J. Phys. Chem. Ref. Data, 19: 677-715.
Simmons, A. C. 1978. The Refractive Index and Lorentz-Lorenz Functions of Propane, Nitrogen and Carbon-Dioxide in the Spectral Range 15803-22002 cm-1 and 944 cm-1, Opt. Commun., 25: 211-214.
Taylor, J. A. 1994. Fossil Fuel Emission Required to Achieve Atmospheric CO2 Stabilisation. Proc., International Symposium of Global Cycles of Atmospheric Greenhouse Gases, Tohoku University, Sendai, Japan, 7-10 March 1994, 308-314.
Thayer, G. D. 1974. An Improved Equation for the Radio Refractive Index of Air. Radio Science, 9(10): 803-807.
Taylor, J. A. 1994. Fossil Fuel Emission Required to Achieve Atmospheric CO2 Stabilisation. Proc., International Symposium of Global Cycles of Atmospheric Greenhouse Gases, Tohoku University, Sendai, Japan, 7-10 March 1994, 308-314.
Terrien, J. 1965. An Air Refractometer for Interference Length Metrology. Metrologia, 1: 80-83.
Trizna, D. B., Weber, T. A. 1982. Brillouin Revisited: Signal Velocity Definition for Pulse Propagation in a Medium with Resonant Anomalous Dispersion. Radio Sci., 17: 1169-1180.
Velsko, S. P., Eimerl, D. 1986. Precise Measurements of Optical Dispersion using a new Interferometric Technique. Appl. Opt., 25: 1244-1349.
Walter, S. J. 1990. Measurement of the Microwave Propagation Delay Induced by Atmospheric Water Vapour, PhD Thesis, Department of Physics, University of Colorado, Boulder, 236 pages.
Xiao, H., Oughstun, K. E. 1998. Hybrid Numerical-Asymptotic Code for Dispersive-Pulse Propagation Calculations. J. Opt. Soc. Am. A 15, 1256-1267.
Zhevakin, S. A., Naumov, A. P. 1967a. Refraction of Millimetre and Submillimetre Radio Waves in the Lower Atmosphere. Radio Engineering and Electronic Physics (translated and published by IEEE), 12(1): 885-894.
Zhevakin, S. A., Naumov, A. P. 1967b. The Index of Refraction of Lower Atmosphere for Millimetre and Submillimetre Radio Waves – The Rotational Part of the Dielectric Permittivity of Atmospheric Water Vapour at Wavelengths greater than 10 Micrometres. Radio Engineering and Electronic Physics (translated and published by IEEE), 12(7):1067-1076.
RESOLUTION No. A
The International Union of Geodesy and Geophysics,
b) the following closed formulas be adopted for the computation of the group refractive index in air for electronic distance measurement (EDM) to not better than 1 ppm with visible and near infrared waves in the atmosphere:
NL = (nL
- 1) ´
106 = 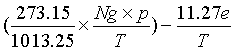
where NL is the group refractivity of visible and near infrared waves in ambient moist air, T is the temperature in kelvin (ITS-90), T = 273.15 + t, t is the temperature in degrees Celsius (°C), p the total pressure in hectopascal (hPa) and e the partial water vapour pressure in hectopascal (hPa).
The group refractivity Ng of standard air with 0.0375% CO2 content at T = 273.15 K ( 0°C ), p = 1013.25 hPa, e = 0.0 hPa is as follows
Ng = (ng -
1) ´
106 = 287.6155 + 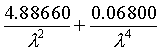
where l is the carrier wavelength of the EDM signal (in micrometre, mm) and ng the corresponding group refractive index.
These closed formulas deviate less than 0.25 ppm from the accurate formulas (see (a) above) between -30°C and +45°C, at 1000 hPa pressure, 100% relative humidity (without condensation) and for wavelengths of 650 nm and 850 nm, for example. The 1 ppm stated before makes some allowance for anomalous refractivity and the uncertainty in the determination of the atmospheric parameters.
Where required, the phase refractivity Nph of standard air with 0.0375% CO2 content at T = 273.15 K ( 0°C ), p = 1013.25 hPa, e = 0.0 hPa may be calculated as follows
Nph = (nph -
1) ´
106 = 287.6155 + 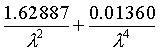
where l is the carrier wavelength of the signal (in micrometre, mm) and nph the corresponding phase refractive index.
Sponsored by the Ad-Hoc Working Group on Refractive Indices of Light, Infrared and Radio Waves in the Atmosphere (convener: J. M. Rüeger) of the IAG Special Commission SC3 on Fundamental Constants (SCFC).
15 June1999
RESOLUTION No. B
The International Union of Geodesy and Geophysics,
b) new absolute measurements of the refractivity of the constituent gases of the atmosphere (incl. water vapour) be carried out at non-laboratory conditions, with special emphasis on near infrared wavelengths.
Sponsored by the Ad-Hoc Working Group on Refractive Indices of Light, Infrared and Radio Waves in the Atmosphere (convener: J. M. Rüeger) of the IAG Special Commission SC3 on Fundamental Constants (SCFC).
15 June 1999
RESOLUTION No. C
The International Union of Geodesy and Geophysics,
Sponsored by the Ad-Hoc Working Group on Refractive Indices of Light, Infrared and Radio Waves in the Atmosphere (convener: J. M. Rüeger) of the IAG Special Commission SC3 on Fundamental Constants (SCFC).
15 June1999