Abstract

This paper summarizes some of the works done in the Special Study Group 3.164 "Airborne Gravimetry Instrumentation and Methods" over the last four years but it does not give a comprehensive overview of all activities. During the last four to five years, major advances in implementing airborne gravimetry as a production system have been made. The LaCoste & Romberg S-model gravimeter has been successfully used for airborne gravimetry by several groups. The inertial scalar gravimetry using inertial system in conjunction with DGPS has also reached a production level. The airborne gravity data over Greenland and parts of the Arctic and Antarctic has been used for determination of earth gravity model EGM96. The local geoid determination using airborne gravity data has achieved excellent results. All these progress shows that the roll of airborne gravimetry in geodesy, particularly in geoid determination, becomes more important.

After the review of the progress in airborne gravimetry, the paper discusses the different techniques for airborne gravimetry. The concept and algorithm to determine geoid, especially the regional or local geoid, using the airborne gravity data combined with other gravity data are also described in the paper. This opens a new subject – airborne geoid mapping, defined as determining geoid using airborne gravimetry data. Test results show that the local geoid determined by airborne gravity data has achieved an accuracy of 5 cm of the geoid undulation. Some important issues in airborne gravimetry and airborne geoid mapping are also included as conclusions.

During the last 4-5 years, major advances in airborne scalar gravimetry as production system have been made. The accuracy and resolution of conventional air/sea gravimeter have been significantly improved. The development of other airborne gravimetry systems has made a breakthrough. The airborne inertial gravity system based on the combination of DGPS and strapdown INS technology has been used in an operational mode.

As the report of IAG Special Study Group 3.164 "Airborne Gravimetry Instrumentation and Methods", the paper first reviews the major progresses in airborne gravimetry, achieved by members of the IAG SSG 3.164. The paper then discusses some important issues in airborne gravimetry development and data processing in more details. Some key techniques of airborne geoid mapping investigated by SSG members are highlighted.

Progress and Activities

First, the principle to airborne gravimetry is briefly described in the following. In general, airborne gravimetry techniques can be classified into:

· Airborne scalar gravimetry,

· Airborne vector gravimetry,

· Gravity gradiometry.

Depending on the approaches to establish the orientation of gravity sensors, the scalar gravimetry system can be divided into four groups:

· Airborne gravimeter based on damped two-axes platform,

· Schuler-tuned platform or inertial platform based airborne gravimeter,

· Airborne inertial gravimetry system,

· Strapdown airborne gravimetry system.

The Review in the following will concentrate on the airborne scalar gravimetry development. The research and development in airborne gravimetry in the last 4 years can be subdivided into two major areas: improvement of conventional airborne gravimeters and development of new airborne gravity systems or integrated airborne systems.

Following accomplishment of airborne gravity survey in Greenland in 1991 and 1992, the US Naval Research Laboratory (NRL) has continued the arctic airborne gravity measurement program during 1992, 1994 to 1997. Under the typical condition for P-3 aircraft, with speed of 450 km/hr and flight altitude of 300-600 m, the NRL airborne gravimetry system, based on LaCoste&Romberg air/sea gravimeter, has achieved an accuracy of about 2 mGal for the wavelength resolution of 10-15 km, Brozena et al. (1997a, 1997b). In 1997, NRL has carried out an airborne flight in the area southwest of San Diego for the experiment with higher resolution (8 km). During the test, three gravimeters, a LaCoste&Romberg S meter, a ZLS gravimeter and Bell BGM—5, were used for comparison of different gravimeters. During last 4 years, NRL has made significant improvements in the measurement system and data processing, Peters and Brozena (1995), Childers (1997).

During 1995/1996, the British Antarctic Survey has undertaken an airborne gravity survey in Antarctic Peninsula area using modified LaCoste&Romberg air/sea gravimeter, Jones (1997).

To extend the Greenland gravity coverage into the permanently ice-covered Arctic Ocean, the National Survey and Cadastre of Denmark (KMS) has carried out the airborne gravity survey in the North Greenland shelf region and the Disko bay using a Lacoste&Romberg gravimeter (S-99) in 1998. By improving data processing, KMS 1998 survey shows excellent results, with an estimated RMS error of 2 mGal for resolution of 6 km, based both on crossover comparisons and independent check with surface gravity data, Forsberg et al. (1999).

During last four years a major progress has been made in the development of strapdown inertial scalar gravimetry (SISG). A prototype of the SISG system was developed by the University of Calgary, based on Honeywell LASEREF III inertial system. Two flight testes were carried out in June 1995 and September 1996. Compared to upward continued ground gravity data and crossover results, an accuracy of 2-3 mGal for the cut-off frequency corresponding to 120 seconds are achieved, Glennie and Schwarz (1997), Wei and Schwarz (1998). Glennie and Schwarz (1999) have compared different inertial systems for the airborne inertial gravity system.

Based on SATR-3i interferometry SAR system, Intermap has developed an airborne inertial gravity system with very high accuracy of gravity measurements, about 1-1.5 mGal for the cut-off frequency corresponding to 120 seconds, compared to upward continued ground gravity data and crossover results, Tennant et al. (1997).

The concept of rotation invariant scalar gravimetry (RISG) based on a triad of accelerometers has been investigated by Wei and Schwarz (1996). This opens an opportunity to develop an airborne gravimetry system without orientation platform. A strapdown airborne gravimetry system using three accelerometers has been developed and is under the test, Boedecker (1997,1998).

One objective of SSG 3.164 is to establish standard data sets for the software development and comparison. The airborne gravity data of the flight test in June 1995 has been published and stored on the University of Calgary FTP site. Many groups have used the test data for the processing development and analysis. Using this test data, OSU group has made prominent progress in the airborne vector gravimetry. Comparing the airborne results with available ground data demonstrates the accuracy of 7-8 mGal for horizontal components and 3 mGal for vertical component, Jekeli and Hwon (1999). This also shows the consistent accuracy of vertical gravity measurements from an airborne inertial gravimetry system using medium-accuracy strapdown inertial system.

Funded by the European Commision, the AGMASCO (Airborne Geoid Mapping System for Coastal Oceanography ) project was carried out in a Noewegian-Danish-German-Portuguese cooperation, Forsberg et al. (1996), Hehl et al. (1997). The objective of the project is to develop an airborne geoid mapping system for the coastal oceanography from combined airborne gravity system/airborne altimetry system. Crossover analysis as well as comparisons with ground truth data shows the accuracy of about 2 mGal over wavelengths of 5-7 km, Bastos et al. (1997).

Organized by the National Survey and Cadastre of Denmark (KMS), the international workshop on "Airborne Gravity and Polar Gravity Field" was held in Kangerlussuaq of Greenland, from June2-4 1998, Forsberg (1998). Following the workshop, a joint test flight for LaCoste&Romber S meter along with inertial gravity unit of the University of Calgary and a strapdown accelerometer system of Bayerische Kommission für die International Erdmessung was carried out. This is first time for the direct comparison of different airborne gravity systems. The comparison of airborne gravity results is under investigation.

Data Processing improvement

The error model for conventional airborne gravimeter and inertial scalar gravimetry is in principle the same. The significant errors affecting airborne scalar gravimetry are expressed as follows

(1)

where  and  are attitude errors,  and  are horizontal specific forces,  is the vertical acceleration error and  is the GPS derived acceleration error. The off-leveling error for the conventional airborne gravimeter is expressed in the tilt direction, see Torge (1989), while equation (1) describes the attitude error in east and north direction.

Equation (1) indicates that the major error sources for airborne gravimetry are attitude-induced error, gravimeter sensor or accelerometer noise, and error of GPS derived acceleration. During last four years, many groups have made lost of effort to improve the correction of attitude-induced errors and reduce the sensor noise and errors in GPS derived acceleration by improving data processing.

Resolution Issue

The resolution of airborne gravity signal is a function of altitude due to the upward continuation effect of gravity signal. The gravity signal will be attenuated as the altitude increases. The resolution of airborne gravity signal describes the characteristics of gravity signal at flight altitude. Assuming the isotropic of the gravity field, the PSD of the gravity anomaly at the flight altitude h can be expressed using the PSD of gravity anomaly on zero level in the following

(2)

where

… the gravity anomaly at the altitude h,

… the gravity anomaly at zero level,

… the Hankel transformation of upward continuation operation.

Equation (2) shows that the airborne gravity signal in the bandwidth of high frequency, or short wavelength, is rapidly attenuated. The RMS power of the airborne gravity anomaly in the bandwidth higher than  can be computed by

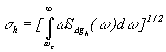(3)

Using the covariance function of the ground gravity anomaly D g, discussed in Moritz (1980), the wavelength corresponding to the frequency can be computed by

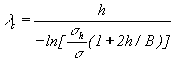(4)

where  is the ratio of RMS power of the airborne gravity anomaly at altitude h and at zero level, B is parameter for the correlation length of the covariance function of gravity anomaly.

In equation (4), the ratio  indicates the attenuation of airborne gravity anomaly. It can be used as the criterion of detectable airborne gravity signal at flight altitude h. The wavelength in (4) can be defined as the minimum wavelength of detectable airborne gravity signal for the ratio . Table 1 gives different wavelengths for the ratio  = 0.5.

Kinematic DGPS solution

During last ten years, differential GPS has been successfully used for the kinematic positioning and navigation. Determining aircraft acceleration from the DGPS solution is a fundamental part for the airborne gravimetry. The error of DGPS solution is still a major or dominated error source for the airborne gravimetry.

Beside the GPS noise, the multipath effect on the GPS observation is other major error source to the acceleration determination. The Study indicated that the mulipath effect on the airborne GPS antenna is somehow randomized due to the aircraft motion. The concept of multiple base stations to reduce the multipath effect and other error sources has been applied to the GPS acceleration determination, Klingelé et al (1997). However, To achieve accurate airborne gravity measurements for the short wavelength, mitigation of GPS multipath effect plays an important roll.

The discontinuity in the GPS solution due to changes in the satellite constellation can cause a significant jump in the GPS derived acceleration. To avoid this problem, the GPS processing for the positioning use should be modified for the acceleration determination. Because of the long distance of the baseline, 200 –500 km, the DGPS solution with floating ambiguities can give better results for the acceleration determination and reduce the discontinuity effect.

The Effect of Attitude Error

Attitude error characteristics depend on the system used for the attitude determination. Because of the short damping period (4 min.), the short term orientation error of the damped two-axes platform of LaCoste&Romberg gravimeter can be considerable big and the influence of the attitude error on gravity results can be significant. However, using horizontal specific force and GPS-derived acceleration, the title of the platform can be estimated. During last 4 years, lots of efforts have been made to improve the correction for horizontal accelerations and off-leveling errors, Paters et al (1995), Childers (1997), Olesen et al (1997) and Forsberg et al (1999). Based on the frequency dependent behavior of the damped platform, determining horizontal acceleration from the accelerometer output has been improved using FFT technique, Olesen et al. (1997).

The short-term attitude errors of an inertial system or Shuler-tuned platform are significantly attenuated due to the Schuler loop with a longer period (84 min.). The misalignment error, which is 10 – 20 arc seconds for a typical medium performance inertial system with DGPS update, will also cause considerable gravity error. The attitude-induced gravity errors depend on both the attitude errors and the specific force as indicated in equation (1). For the scalar gravimetry, only the horizontal accelerations have to be considered. The low-pass filtering will significantly reduce the effect of the phugoid motion on the horizontal acceleration, when the oscillation frequency of the phugoid motion is higher than the cut-off frequency of the filtering. For the straight flight line with constant speed, the specific force in the horizontal channel can be approximately a constant due to the Coriolis and centrifugal acceleration for 20-30 min flight. Within this time period, the attitude error of inertial system can be considered as a bias or linear drift. Therefore, the attitude-induced gravity error in interested bandwidth can be described by a first-order polynomial function, and estimated using crossover adjustment method.

Filtering Technique

To reduce the effect due to the differentiation process and measurement noise, the filtering technique is usually applied to the airborne measurements. There are three types of filtering algorithms used for the airborne gravity measurements. They are:

· Infinite impulse response (IIR) low-pass filtering,

· Finite impulse response (FIR) low-pass filtering,

· Model-based filtering approaches.

The IIR and FIR low-pass filter are frequency based filters and used for most airborne gravity processing. When a low-pass filter is applied, the useful gravity signal, gravity anomaly, is preserved in the bandwidth of low frequency. The advantage of using low-pass filtering is easy implementation and its spectral characteristics. Designing and applying a low-pass filter to the airborne measurements plays a fundamental roll in the airborne gravity processing. During last four years, an effort has been focused on improvement of the effeteness of low-pass filtering. The team of US NRL has combined R-C filter with a FIR filter to sharpen the frequency rolloff, Childers et al. (1997). The group of KMS of Denmark has design a new Butterworth filter for the airborne gravity data, Forsberg et al (1999). The FIR filter is applied to the inertial gravimetry data by the U of C and used for Intermap airborne inertial gravimetry system.

However, the low-pass filter is a non-model filtering technique. The signal and noise in the bandwidth of high frequency are attenuated when the low-pass filtering used. Thus, the useful gravity signal in the bandwidth of high frequency will be lost and the noise in the pass band remains. Besides the low-pass filtering, the model-based filtering approaches have been applied to the airborne inertial gravimetry measurements. This approach is based on the Kalman filtering and wave approach. The model-based filtering has been successfully applied by the LIGS group, Salychev (1995). The comparison between frequency based filtering and model-based filtering was investigated by Hammada and Schwarz (1997).

Airborne Geoid Mapping

The major contributions of airborne gravity measurements in geodesy are determination of the earth gravity model and local geoid determination. The airborne gravity measurements over Greenland and part of Arctic have made significant contribution to the global gravity model EGM96, Lemoine et al. (1996, 1998), Kenyon (1998).

In recent years the airborne gravity measurements are used for the determination of precise local or regional geoid, Forsberg and Brozena (1996), Kearsley et al. (1998), Wei et al. (1998). Comparing to the independently determined geoid shows that the accuracy of 5-10 cm for the geoid undulation determined by using airborne gravity measurement combined with global gravity model and terrain information can be achieved, Kearsley et al. (1998), Wei et al. (1998). Thus, the airborne gravity derived geoid can be used as precise vertical reference of orthometric height. This provides an efficient way to determine orthometric height without traditional leveling.

The principle and technique to determine the local or regional geoid using airborne gravity measurements has been described in Forsberg and Brozena (1996). The remove-restore technique is applied to minimize the errors due to limited spatial size. This method combines the airborne gravity measurements with global gravity model and surface terrain information.

The downward continuation of either airborne gravity anomaly or airborne geoid undulation plays a key roll in geoid determination using airborne gravity data. In principle, there are two downward continuation methods:

· FFT downward continuation technique,

· Least-squares collocation method.

As indicated in equation (2), the downward continuation is a very unstable process. Both the signal and noise in the high frequency bandwidth will rapidly increase by a downward continuation procedure, particularly for the higher flight altitude. To reduce the noise in the high frequency bandwidth, a filtering or smoothing technique is applied to the FFT downward continuation, Forsberg and Kenyon (1995). The regularization method can also be applied when the FFT downward continuation technique is used. The collocation method can be implemented in either spectral domain or spatial domain, Sideris (1995), Tscherning et al. (1997). The FFT downward continuation method provides an easy and fast process scheme. The advantage of collocation method is the possibility of combination with ground data or other heterogeneous data.

Other issue for downward continuation is the resolution of the airborne gravity derived geoid. As discussed above, the wavelength of detectable airborne gravity signal is determined by the flight altitude. The resolution of the geoid undulation computed by airborne gravity signal is also determined by the upward continuation characteristics.

During the last 4 years major progress in airborne gravimetry has been made. The accuracy and resolution of conventional airborne gravimeter have been significantly improved. The airborne inertial gravity system has been developed with competitive accuracy and used in an operational mode. Under the normal operational condition, an accuracy of 1-3 mGal over wavelength of 5-10 km for the airborne gravimetry system has been achieved.

The contributions of airborne gravity data with current accuracy to the geodesy become more important. The gravity data over Greenland and part of Arctic have provided significant improvement to the current global gravity model EGM96. Using the airborne gravity measurements, an accurate local geoid can be determined and used as a height reference. This leads to a new subject – airborne geoid mapping.

It is still very difficult to achieve a performance of 1-2 mGal over 1-2 km wavelength using the current airborne scalar gravimetry technique, to meet the requirement of geophysical exploration application. Error in GPS-derived acceleration using current GPS technique and processing algorithm seems to limit the accuracy of acceleration over short wavelength. When the cut-off frequency of low-pass filtering is higher than the frequency of the phugoid motion, the effect of the phugoid motion can be a critical issue and should be investigated.

Other way to increase the spatial resolution of airborne gravity data is combining airborne gravimetry system with a gravity gradiometer, as proposed by NRL, Brozena et al. (1997). This will merge the medium wavelength gravity signal with the short wavelength gravity information.

The downward continuation of either airborne gravity anomaly or airborne geoid undulation for the airborne geoid mapping needs more investigation, particularly for the mountain area. If the airborne gravity measurements are combined with ground gravity data or other gravity data, the question of optimization of the gravity data with different spectral bandwidth should be investigated.

First of all, I would like to thank all members of IAG Special Study Group 3.164 "Airborne Gravimetry Instrumentation and Methods" for the contributions to the progress in airborne gravimetry. The contributions of many members to this report are specially acknowledged.