The work of the SSG 1.154 on "Quality Issues in Real-Time GPS Positioning" will focus on identifying practical procedures, as well as mathematical techniques, that can be applied to assure the quality of positioning results obtained from this distinct class of GPS applications. The objectives of the SSG therefore were identified as being: (a) IDENTIFY the main issues impacting on the "quality" of real-time GPS positioning -- including those due to instrumental effects, environmental sources, site-dependent effects, communcations-dependent, etc.

(b) COMPILE a set of procedures, algorithms and guidelines that can be implemented within real-time GPS positioning software -- this is the practical outcome.

(c) DEFINE areas for further research and development -- as derived from both practical experience, and a study of the literature and research trends in the development of mathematical and/or empirical tools for "quality control".

In hindsight it would appear that this was a very ambitious set of objectives for the SSG. In this report, in subsequent sections, this theme of noble and wide-ranging objectives not being matched by outcomes will be raised again and again.

1.2 Tasks to be Undertaken

The abovementioned objectives were translated into a series of tasks: 1) Compile and document the QC procedures and algorithms as implemented in scientific GPS geodesy software.

2) Investigate which of these procedures are adaptable for "real-time" operation -- for example, for the detection of faulty navigation messages, data spikes, etc.

3) Compile a bibliography of D-I-A literature specifically applicable to precise real-time kinematic GPS positioning.

4) Research fault detection algorithms for real-time GPS applications.

5) Encourage discussion and critical evaluation of such algorithms.

6) Monitor the activity taking place in the development of quality control (QC) and quality assurance (QA) for standard pseudo-range based DGPS.

7) Determine the appropriate "mix" of QC/QA procedures that can be recommended for real-time precise GPS positioning -- as it is was felt that a "cocktail" of procedures will be necessary to give greatest assurance on quality.

8) Prepare a report on the SSG's activities and recommendations.

 
 

1.3 SSG Membership

As of June 1999, the SSG membership was (see §A.1):

C. Rizos (Australia) President

H. Abidin (Indonesia)

J. Behr (USA)

E. Cannon (Canada)

P. Collins (Canada)

R. Galas (Germany)

S. Han (Australia)

Y. Hatanaka (Japan)

X. Jin (Switzerland)

H. Kutterer (Germany)

Y. Li (Canada)

S. Mertikas (Greece)

P. Morgan (Australia)

S. Oszczak (Poland)

W. Roberts (United Kingdom)

G. Seeber (Germany)

M. Stewart (Australia)

L. Wanninger (Germany)

Was the composition of the membership ideal to undertake this task? It could be argued that voluntary membership of an IAG SSG will never bring together the most appropriate expertise and interests. It is one of the roles of the Chairman of the SSG to select (or recruit) the membership according to criteria that ensure the "best" people are coopted. If the focus of the SSG were narrower, then the membership could "select itself", by simply inviting the handful of "experts" and "active researchers" to the SSG. It would then be expected that this mix of theoreticians and experimeters (or "number crunchers") would generate the environment in which active discourse and detailed studies could be promoted. (With email contact, certainly the geographic separation of the SSG members could no longer be held to be a constraint on scholarly activity.) In reality, the selection of members was not a careful and scientific process.

The membership list contains mostly academics, graduate students and government employees. Yet the only real-time, carrier phase-based GPS positioning systems are commercial products. The small number (just two) of members drawn from private industry could be construed as a glaring shortcoming. However, it is debatable whether scientists employed by GPS manufacturers would be able to freely contribute their expertise and knowledge to the SSG. Another group that, in hindsight, is underrepresented (again by just two members) are staff from the geodetic departments that deal, on an everyday basis, with the processing of data from permanent GPS networks such as SCIGN (USA) and GEONET (Japan). Although they would not be dealing with "real-time" processing, the issue of "quality control" would certainly be addressed on an institutional basis.

1.4 Comments to the SSG Research Agenda

Before dealing with explicit outcomes, it is appropriate to make some comments on the rationale behind the SSG's original research agenda, and to comment on its shortcomings: 1) At the time of the establishment of the SSG the Chairman had suggested the following characteristics that distinguish those real-time positioning techniques that would be the focus of study from those that would not: • the communication of data from GPS receivers to a computing site where it is processed with no, or minimum, delay,

• make use of carrier phase data,

• rely on data processing on an epoch-by-epoch basis, or at the very least small "batches" of GPS data,

• do not permit extensive data "pre-processing" or the review of data and results in iterative procedures, and

• may involve kinematic or static positioning.

2) One of the first tasks of the SSG (§1.2) was to compile and document the QC procedures and algorithms as implemented in scientific GPS geodesy software. It was reasoned that because this type of data processing is at the most sophisticated level, it would be expected that they would be the most highly developed. The comment was made that it was likely that these procedures were largely "empirical" and based on extensive experience gained working with GPS data, and that they were unlikely to be documented in the available literature. Members of the SSG did have experience with a range of scientific GPS geodesy softwre packages. After several prompts, some members did come forth and volunteered their knowledge of QC procedures, and it was clear that these were indeed in the category of empirical "rules-of-thumb" and were not founded on a well developed mathematical basis. What correspondence the Chairman did receive was compiled into email SSG memos for the benefit of the other SSG members, and can be inspected by all through a visit to the SSG's website (§2.2). Given that several IGS Processing Centres now have many years of experience in the automatic processing of large volumes of GPS data on a daily basis, it is disappointing that the QC procedures are not well defined or documented.

3) The next step was intended to be the investigation into which of these procedures are adaptable for "real-time" operation. This would "bridge" the pragmatic procedures based on such criteria as size and distribution of "data gaps", signal-to-noise ratio values, faulty navigation messages, data spans for which both L1 and L2 data were available, ionospheric activity (as indicated by L1/L2 combinations), etc., with the highly developed "fault detection" algorithms associated with digital signal processing in general, and the D-I-A procedures implemented in navigation software. This would be at the "heart" of the SSG's activities. Unfortunately very few members had the requisite background in signal processing, reliability theory, D-I-A algorithms and statistical testing to make contributions. Several members did indeed make significant contributions, and the Chairman acknowledges their contribution (§2.1). One of the important outcomes of the SSG was to be the compilation of a bibliography of D-I-A literature specifically applicable to kinematic GPS applications. One member of the SSG did compile a list of general references to fundamental literature on "fault detection", statistical testing, and the like (see §2.3 and §A.2). However, the Chairman was remiss in not updating this list with literature that specifically dealt with its application to kinematic GPS positioning.

4) It was recognised from the start by the Chairman that the current "best practice" was that applicable to pseudo-range-based differential GPS (DGPS). The first real-time applications addressed by GPS were those for differential positioning using transmitted pseudo-range corrections (generated by a stationary reference receiver located on a known site). The SSG was fortunate that one member was closely involved in the development of QC practices for DGPS for the offshore industry. It was reasonable to conclude that the SSG could learn from that experience, and in many respects to emulate the process, but in relation to carrier phase-based positioning. Emails were exchanged between SSG members, and the relevant correspondence was summarised and place on the SSG's website (§2.2). The following comments were made at the time (and are still valid today): • While not within the direct interest of this SSG, "quality control" for real-time DGPS is a useful starting point because of the extensive activity in this area over the last few years.

• A recent study of "quality measures" for DGPS has identified many factors impacting on quality that cannot be overcome by mere recourse to new mathematical algorithms. "Quality" is something that must be viewed as being somehow a holistic concept that requires "quality management" to be at its core. Hence attention must also be paid to many other non-mathematical issues such as equipment quality (certification? cabling and antenna quality), communications reliability and integrity, site-specific disturbing effects, hardware/software calibration procedures and maintenance schedules, and even operator training.

• A holistic study of GPS quality is likely to be well beyond the expertise of this SSG. However, the partitioning of error sources into distinct categories, permitting a "targetted" effort to address each error sources using appropriate tools, should be attempted. Hence recommendations on improving real-time GPS positioning quality are likely to include the definition of a "cocktail" of tools, some with the rigorous mathematical basis (e.g. "data-snooping" techniques), while others may be essentially derived from empirical analysis.

5) From the very beginning the SSG Chairman held the view that a "mix" of Quality Control and Quality Assurance procedures would be needed for real-time precise GPS positioning. However, unfortunately one of the outcomes of the SSG's work is a rather incomplete list of QC issues that need to be addressed if fast, reliable, real-time, centimetre accuracy GPS positioning results are to be assured close to 100% of the time (§3). It became obvious with time that the expertise of most SSG members was in improving the efficiency and reliability of "on-the-fly" (OTF) ambiguity resolution (AR), a critical step in making high precision kinematic GPS positioning. Hence the technical issues associated with OTF-AR became the focus as these were "quality control" issues in the classic mathematical/statistical sense. However, the holistic QC approach had to be shelved.

  1.5 Administrative Issues

At the time the SSG was established the Chairman had some thoughts on how the SSG could function. It is worth mentioning them here, and to indicate how some of the reasons for the SSG not fulfilling its ambitious agenda can be traced to a failure to provide the appropriate leadership at crucial times.

In an ideal world a SSG consists of a small group of dedicated researchers, drawn together by their interest in, expertise of and everyday involvement with the topic under study. Once the Chairman defines the scope of the topic and deals with the procedural matters concerning membership, etc., the SSG would then provide a forum for the exchange of ideas and the reporting of the results of new investigations. The members would be able to collectively push forward the frontier of knowledge, and the Chairman's role would be to report progress to the wider IAG community.

In reality the members of the SSG come from different backgrounds, and have varying levels of interest, experise and involvement in the topic area. A small core may be identified as being particularly active, but the others may only contribute occasionally, if at all. The core participants may communicate regularly (particularly by email), and often without involving the Chairman. Although it could be reported that "progress was made", it would be difficult to disprove the claim that such progress would have been made even without the formation of the SSG. So what can an SSG realistically accomplish? • The appointment of an SSG in an area sends a "signal" that the IAG recognises the importance of this area of work.

• The SSG can focus light on the disparate activities that may be taking place and organise specialised session at conferences where the work of investigators can be presented to the wider geodetic community.

• The SSG may initially introduce an investigator in one country to colleagues in other countries who are undertaking similar activities (less likely these days given the volume of published literature and the ubiquitous use of the Internet).

• The SSG report can be a valuable resource for system developers who wish to implement the recommendations concerning algorithms and procedures, or for investigators to continue the research work.

• For those within the SSG, there is the possibility of obtaining direct access to up-to-date reports and results (only if the SSG contains active researchers in the area of interest).

Clearly how well the SSG functions (the SSG could be deemed satisfactory if at least some of these functions are fulfilled) is very much dependent on the efforts and talents of the Chairman and individual members of the SSG. So what can an SSG NOT do? • It cannot commission studies in the conventional, prescriptive sense (afterall, the members are volunteers).

• It cannot function as an "advisory board", dispensing advice and "remedies" to individuals or organisations.

• It cannot force the SSG members to collaborate when they chose not to, or for various reasons are unable to.

• It cannot insist that SSG members divulge sensitive information and data to other members before the normal processes of publication or patent submission.

• It cannot force SSG members to attend conferences and meetings.

The Chairman's task is in many ways a thankless one. For many SSGs, no matter how well meaning and idealistic everyone is in the first months after the formation of an SSG, enthusiasm often wanes alarmingly. If this is not checked, then by the end of the four year life of the SSG the only person contributing is the Chairman, and his contribution is an insipid report to the IAG. He (or she) may have grown disillusioned as his/her repeated exhortions to SSG members to contribute literature, recommendations or even opinions for inclusion in the final report are largely ignored. How does one guard against this? One suggestion is to keep the work of the SSG "focussed" on a single well-defined issue. How does one define a "focussed" topic for the SSG? Already, even a cursory study of the "quality issues in real-time GPS positioning" would raise an alarm. A suggestion may be to: • Pepare a report that reflects the diversity of the topic "quality issues in real-time GPS positioning".

• Report on specific algorithms or procedural developments that are practical and immediately useful.

The first requires that the Chairman take a lead, and that members of the SSG contribute: (a) ideas and advice on the structure and content of the report, and (b) bibliographical lists. At this level the report can be viewed as a well researched "plan-of-action". In the context of this SSG, even if it just contains a clear definition of terminologies, a comprehensive catalogue of error sources, a summary of mathematical techniques (with their assumptions clearly stated), quality guidelines of a "non-mathematical" nature, supported by a comprehensive bibliography, then one would be satisfied that the SSG had succeeded in fulfilling one of its objectives.

The second is the more traditional function of an SSG, i.e. the reporting of work of the members of the SSG as well as of others known to the members. This is done through conference presentations, SSG internal discussion channels, and remaining alert to developments appearing in the literature. However, preference must be given to practical developments, i.e. those that can be tested, implemented and used unambiguously by others beyond the SSG.

The members of the SSG are drawn from many backgrounds, and from as wide a geographic spread as possible. What this SSG does not have in significant numbers are members from the GPS industry who are responsible for the development current real-time kinematic systems. It could be argued that our SSG (in fact the IAG) suffers by not having such members. While the SSG Chairman can picture himself/herself as an orchestra"conductor", the SSG members cannot be considered to be at his/her "beck and call". The SSG members could be expected to contribute in the following manner: • Thoughts, suggestions and advice (both solicited and unsolicited) on the topic of QC and QA.

• Submitting to the Chairman, and other SSG members, copies of relevant reports and publications that they have prepared.

• Drawing attention to the SSG relevant articles or research activity that they may have become aware of.

• Participating in sessions at conferences that this SSG may chose to organise.

• Respond to specific requests by the Chairman.

Even a cursory glance at the above comments, and a study of the outcomes and achievements in the next section, would indicate that this SSG has failed to achieve the (admittedly unrealistic) objectives that it set itself. It could be argued that this failure is partly due to the SSG Chairman not completing the tasks that he set himself, as well as a membership that does not have sufficient experience in developing real-time positioning systems.

 
2. OUTCOMES AND ACHIEVEMENTS

2.1 Communications

Communications is what makes possible the SSG's activities. The Chairman has periodically written memos that have been sent to members by email. These have also been placed on the SSG's web site (§2.2). While this communication is necessary the more "productive" communications is between SSG members (to which the Chairman cannot comment on) and feedback from individual SSG members to the Chairman. There are members who have corresponded with the Chairman, and who have contributed to discussions, and there are members who have played almost no part in the SSG communications. Only 6 memos were written by the Chairman, however many more emails were sent to individual members asking for their comments and advice. Some correspondence was also had with non-members. The last Chairman's memo was written in early 1998.

The following is a summary of the correspondences: • M. Stewart & J. Wang -- papers and draft documents on "empirical" QC procedures, mathematical techniques for GPS+Glonass AR and validation procedures, modification of stochastic models, system modelling in Kalman filters.

• W. Roberts -- definition of "quality", UKOOA QC guidelines, shortcomings of DGPS QC, stochastic modelling, statistical testing, ideas for carrier phase-based procedures.

• Y. Hatanaka -- orbit issues, broadcast vs IGS precise ephemerides, scientific softwre data screening procedures.

• L. Wanninger -- ionospheric disturbances, mitigation of biases using multiple reference station techniques.

• S. Mertikas -- definition of "quality", development of fault detection algorithms, quality "measures", co-authored several papers with Chairman.

• H. Kutterer -- terms of reference of the SSG, QC procedures within the Bernese scientific GPS software, experiences with RTK with the Trimble receiver, GPS signals through forest foliage.

• S. Han, L.S. Lin -- ambiguity resolution and QC & validation procedures, strategies for mitigating residual biases for short, medium and long-range GPS positioning, multipath, ionospheric studies, data communication latency issues.

• F.K. Brunner -- literature related to data quality and modelling.

 

2.2 Web Site

One of the most important outcomes was the establishment of a web site by the Chairman. The URL is: www.gmat.unsw.edu.au/ssg_RTQC. The site contains the terms of reference, the text of the Chairman's memos, membership details, as well as email messages received from members that might be of interest to the general community. The SSG bibliography is a HTML document on the web site. This report can be downloaded as a PDF file from the web site.

2.3 Bibliography

Development of a bibliography of relevant literature was identified as an important objective of the SSG. One member, S. Metikas, compiled a bibliography of general references to statistical testing, quality control, fault detection, etc., that forms a valuable resource. However, the compilation of a similarly detailed bibliography focussing on the literature dealing with the techniques of carrier phase-based, kinematic GPS positioning has not been carried out. This remains, in the Chairman's opinion, one of the greatest failings of the SSG.

2.4 Miscellaneous

As stated elsewhere, the objectives of the SSG were ambitious. By attempting to go for the all-encompassing approach of "quality control", more achievable (though perhaps minor) objectives could not be systematically addressed. Yet it is conceded by most investigators that "quality control" is an ever more important issue as high precision GPS kinematic strives to do "more with less". That is, less data to achieve similar levels of performance (measured in terms of accuracy and reliability). Hence the traditional fields of investigation of on-the-fly (OTF) ambiguity resolution (AR) have in fact contributed more to QC studies than would have been expected. The literature on "QC issues for real-time kinematic positioning" is dominated by papers dealing with OTF-AR techniques, and in particular the validation procedures that must guard against wrong AR. These validation procedures have forced a closer study of "data quality" in general. Hence, QC not only deals with the results, but also identifying the conditions at the data capture stage that assure "good quality data". Unfortunately no objectives "quality measures" have been defined for "data quality", although some, such as signal-to-noise ratios, have been proposed.

Site specific influences on data quality are important, particularly the multipath disturbance. However, other SSGs in fact deal with topics that overlap the terms of reference of this SSG (e.g. SSG 1.156 Advanced GPS Analysis for Precise Positioning, SSG 1.157 GPS Ambiguity Resolution and Validation, SSG 1.1.58 GPS Antenna and Site Effects). In the opinion of the Chairman, the "blueprint" for a quality "audit" is the UKOOA study on QC guidelines for DGPS in the offshore industry.

Finally, although big strides have been made in improving AR and validation, there is little experience of real-time implementation of QC procedures. In the Chairman's opinion this is a serious failing of the SSG. No member had intimate knowledge of how to establish, "from the ground up", a real-time, kinematic GPS positioning system. Hence the work that can be acknowledged is piecemeal and generally relates to QC for OTF-AR at the data processing level. What is ignored are the various components and algorithms for signal tracking (including signal processing within the GPS receiver), site location and its influence on data quality, data link issues, base (or static reference) receiver issues. In order to go someway towards redressing this failing, the Chairman has described the issues that had to be addressed in the development of two real-time or "near"-real-time systems capable of supporting carrier phase-based, kinematic GPS positioning.

 
3. QC ISSUES IDENTIFIED AS BEING CRUCIAL FOR FURTHER STUDY

Real-time, carrier phase-based GPS positioning techniques are now increasingly used for many surveying and precise navigation applications on land, at sea and in the air. Quality control (QC) issues have to be addressed at different stages of the GPS positioning process, for example, data collection, data processing and data display. In this section, the quality control procedures or methodologies for the following critical operations are discussed: • Measurement quality control for single receiver data, concerned with issues such as failured satellites, ionospheric scintillation, multipath and cycle slips.

• Quality assurance for data communication and data transmission delay.

• Quality control of the position modelling procedure, related to systematic error mitigation and stochastic modelling.

• Ambiguity resolution and validation procedures

As examples, the proposed quality control procedures to be implemented in: (a) the Singaporean multi-base station network, and (b) the GPS-based volcano deformation monitoring system in Indonesia are described, and future or unresolved considerations are outlined. The aim of this is to indicate the range of issues that would need to be considered by the SSG, by using specific examples of systems under development at the Chairman's institution, the University of New South Wales, Sydney, Australia. The Chairman acknowledges the valuable work done in this area by his colleague, and SSG member, Dr. Shaowei Han.

 
3.1 Quality Control for Data Logging Quality Control Issues at a Single Receiver Site

The following are some of the QC issues that impact on data logging from a single receiver:

• Detection of failed satellites

• Ionospheric activity

• Multipath disturbances

• Cycle slip detection and repair using one-way data

Although GPS satellites are quite reliable, the failure of satellites is not an uncommon occurrence. The GLONASS satellites fail more regularly. Satellite failure could be indicated by the broadcast navigation message, signal being missing, measurement signal-to-noise ratio too small, or measurement "quality" (an admittedly vague term). However, the pseudo-range measurement quality could be judged by a point positioning procedure if more than four satellites are available. A procedure for scanning the raw observation data based on using a Kalman filter to model the behaviour of phase and phase-rate measurements (and their changes) in discrete time is described in, for example, Mertikas & Rizos (1997). This procedure can be applied to each of the data types separately. The information from different receivers provides the external check for the satellite failure.

Ionospheric delay could be estimated by pseudo-range and carrier phase data. If a single-frequency receiver is used, the difference between pseudo-range and carrier phase could be used to estimate the ionosphere delay (Qiu, et al, 1995). However, the dual-frequency data offers especially rich opportunities to construct combinations of observables (phase-only, pseudo-range-only, as well as phase and pseudo-range) (e.g., Rizos, 1997) which may be screened using a number of procedures based on Kalman filters of various types, trend-following polynomials, digital filters, and so on. Ionospheric disturbances, which can occur suddenly and can be very severe, affect the amplitude and phase of GPS signals (Wanninger, 1993; Knight & Finn, 1996). One of the phenomena responsible for these are "travelling ionospheric disturbances", another is due to irregularities in the ionosphere causing "scintillations" (especially in the tropical and auroral zones). Under such conditions the ionosphere is so perturbed that single-frequency operations may become impossible because the GPS receiver loses lock on the satellite signals. Where tracking is possible, the likelihood of cycle slips and interrupted tracking is increased, both of which, for example, make ambiguity resolution a more difficult and unreliable task. Knight & Finn (1996) describe an algorithm for determining the so-called S4 "scintillation index". Empirical filtering techniques will need to be developed to cope with such effects in real-time, particularly when the next solar cycle maximum occurs at the turn of the century.

Multipath is a signal disturbance arising from the fact that the signal entering the GPS antenna, in addition to containing the direct satellite-receiver component, also includes reflections from buildings, water surfaces and the ground. Multipath and diffraction effects cannot be easily accounted for during data processing. Fortunately the multipath error on carrier phase observations is significantly less than that experienced on pseudo-range data (of the order of several centimetres, compared with metre level disturbance on pseudo-ranges). Furthermore, its effect tends to average out for static baseline determinations with observation sessions of the order of an hour or more. Nevertheless, for the highest precision static and kinematic applications the effect of multipath disturbance must be addressed. The multipath component in the L1 and L2 pseudo-range data can be estimated (Rizos, 1997). The multipath error in carrier phase cannot be estimated from the raw measurements on a single receiver basis, but may be estimable on a baseline basis from the double-differenced residuals after baseline processing. In the case of a reference receiver, the geometry of the satellites, relative to the receiver and surrounding reflective objects, is almost exactly the same after one sidereal day. Hence the multipath disturbance tends to exhibit a daily signature, both in the raw measurements and in the baseline residuals. So-called "multipath-templates" can be constructed to correct pseudo-range measurements, from an analysis of the past one or more day's data, or to correct the double-differenced carrier phase measurement (Lin & Rizos, 1997; Han & Rizos, 1997a). The SIGMA-model was suggested by Brunner et al. (1999) and Hartinger & Brunner (1999), which using the measured signal-to-noise ratio (S/N) data and a template technique to derive a proper variance for all phase data in order to improve the positioning results. However, apart from mathematical procedures there are several strategies for overcoming the problem of multipath in the observations at permanent GPS receivers: • Careful selection of site in order to minimise the multipath environment.

• Use of multipath resistant antennas.

• Use special receivers that contain "multipath elimination tracking technology".

• If it is possible, multipath should be corrected at each receiver.

Cycle slips are discontinuities of an integer number of cycles in the measured (integrated) carrier phase resulting from a temporary loss-of-lock in the carrier tracking loop of a GPS receiver. This corrupts the carrier phase measurement, causing the unknown ambiguity value to be different after the cycle slip compared with its value before the slip. It must be "repaired" before the phase data is processed as double-differenced observables for GPS surveying techniques. GPS manufacturers have used different techniques to repair cycle slips before the carrier phase measurements are processed. A procedure for scanning the raw observation data based on using a Kalman filter to model the behaviour of phase and phase-rate measurements (and their changes) in discrete time developed by Mertikas & Rizos (1997) could be used for this purpose. Ambiguity recovery techniques used for long-range GPS kinematic positioning by Han (1997a) could also be used for cycle slip detection and repair using one-way data.

Implementation of QC Procedures at a Single Site

Different software packages to implement QC procedure and to indicate the quality of data were developed by GPS manufactures and others, e.g. TEQC by UNAVCO, EVALUATE by Ashtech. The University of New South Wales, in conjunction with Australian Defence Science and Technology Organisation, is developing a QC system which could be used for data logging and indicating data quality. The cycle slip detection and repair procedures based on the algorithms of Mertikas & Rizos (1997) and Han (1997a) are implemented. The multipath-template for multipath is also generated. Another feature is that the system is able to detect, track and indicate ionospheric scintillation in real-time. A fuzzy expression for scintillation intensity has been used to overcome the ambiguity existing in the numerical and linguistic definition and to provide an indication of scintillation intensity.

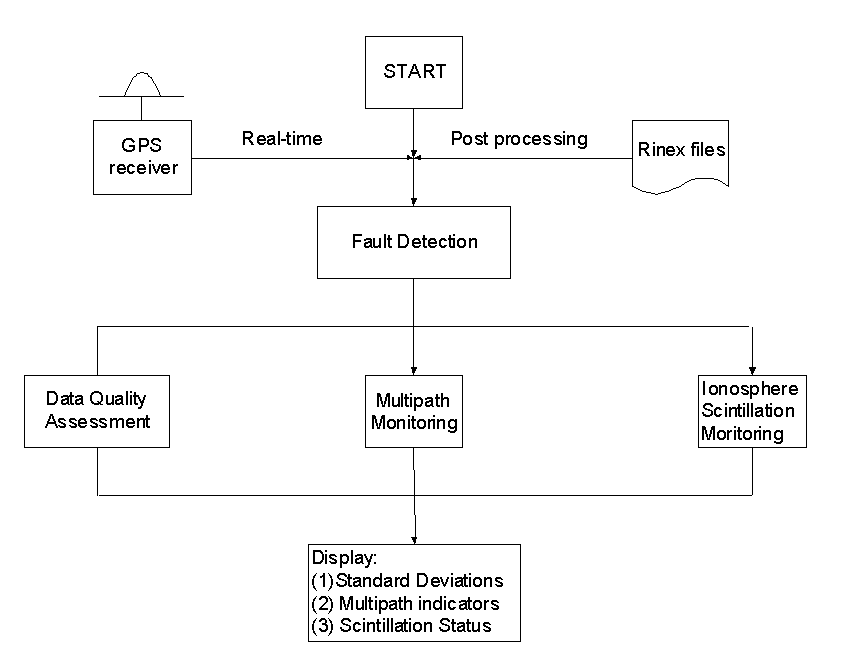
The data flowchart is illustrated in Figure 1. The input can be from GPS receivers directly, referred to as the "Real-Time Mode" or from the RINEX files, referred to as the "Post-Processing Mode". The raw data are then scanned to detect all jump outliers, such as cycle slips in carrier phase measurements. Two algorithms proposed by Mertikas & Rizos (1997) and Han (1997a) are used. In order to give the measurement standard deviations, multipath significance, and ionospheric scintillation status, three components, which are called data quality assessment, multipath monitoring and ionospheric scintillation, are then introduced. For continuous GPS reference stations, the computer facility, e.g. harddisk, power, etc. should be also considered for quality assessment and QC.
 

Figure 1. Implementation of QC Procedure on a Single Site

3.2 Quality Assurance for Data Communication

Communication Format, Data Rate, and Latency

The United States body, the Radio Technical Commission for Maritime (RTCM) Services, is a group concerned with the communication issues as they pertain to the maritime industry. Special Committee 104 was formed to draft a standard format for the correction messages necessary to ensure an open real-time DGPS system (Langley, 1994). The format has become known as RTCM 104, and has recently been updated to version 2.2.

The RTCM SC-104 message types 18 to 21 provide for RTK service, however the awkwardness of the format and their message frame "overhead" make them relatively inefficient for RTK. For example, to satisfy once per second data transmission for RTK, a baud rate of 4800-9600 would be required (the higher baud rate would be required if DGPS correction messages are also sent), quite a technical challenge, and even more so if radio repeaters have to be used (for each repeater employed, the data rate must be doubled).

As a consequence, GPS-RTK manufacturers have designed their own proprietary data transmission standards to overcome the RTCM problems. One which had been used by the Trimble RTK systems for several years, has been proposed as an "industry standard" (Talbot, 1996). This format is referred to as the Compact Measurement Record format. It uses an efficient compression/decompression algorithm which makes it suitable for communications links that run at 2400 baud, and still deliver once per second GPS solutions. The latest version of RTCM-104 may make redundant such a need for an "industry standard" that is based on a single manufacturer’s format.

Different countries have different regulations governing the use of radios, their frequency and power, hence there is considerable opportunity for confusion. In Australia, the Spectrum Management Agency is responsible for issuing permission on the use of selected radio frequency bands for data communication. In general, the UHF and VHF bands are favoured for RTK applications, in particular the "land mobile" band, 450-470 MHz. The maximum power is dependent upon the type of licence issued to the user, and may range from about 5 W for roving users, to 50 W for fixed local sites. There is a complex relation between: height of transmitting antenna, the type of antenna used (Yagi or omnidirectional), transmitting power, cable length, tree cover and other intermediate objects; and the range of the radio. For test/demonstration purposes up to a few kilometres, a 1 W transmitter operating within the UHF "land mobile" band, should be adequate if the site conditions are ideal.

Data latency problems for RTK can be resolved in either of the following two ways: (a) synchronise reference receiver data and mobile receiver data (which gives the maximum precision but a substantial delay), or (b) use the latest reference receiver data and extrapolate them to the time of the mobile receiver data (which will cause some additional error). The former is better for the carrier phase ambiguity resolution process, as all errors have to be minimised for maximum reliability and performance. However, the kinematic position will suffer due to a time delay of up to 1-2 seconds (which may be crucial for some real-time applications). The latter solution will introduce additional errors due to observation extrapolation. Experimental results show that the linear extrapolation model will introduce an additional double-differenced error of about 2cm for a 1 second delay and about 8cm for a 2 second delay. A quadratic extrapolation model will introduce an additional double-differenced error of about 4cm for a 2 second delay (Landau, et al., 1995; Lapucha, et al., 1995).

Communication Link Considerations

The following considerations must be addressed by DGPS/RTK communication links: • Coverage: This is generally dependent on the frequency of the radio transmission that is used, the distribution and spacing of transmitters, the transmission power, susceptibility to fade, interference, etc.

• Type of Service: For example, whether the real-time DGPS/RTK service is a "closed" one available only to selected users, whether it is a subscriber service, or an open broadcast service.

• Functionality: This includes such link characteristics as whether it is a one-way or two-way communications link, the duty period, whether it is continuous or intermittent, whether other data is also transmitted, etc.

• Reliability: Does the communications link provide a "reasonable" service? For example, what are the temporal coverage characteristics? Is there gradual degradation of the link? What about short term interruptions?

• Integrity: This is an important consideration for critical applications, hence any errors in transmitted messages need to be detected with a high probability, and users alerted accordingly.

• Cost: This includes the capital as well as ongoing expenses, for both the DGPS/RTK service provider as well as users.

• Data rate: In general the faster the data rate, the higher the update rate for range corrections, and hence better positioning accuracy. Typically a set of correction messages every few seconds is acceptable.

• Latency: Refers to the time lag between computation of correction messages and the reception of message at the rover receiver. Obviously this should be kept as short as possible, and typically a latency of less than 5 seconds is suggested.

• Quality assurance for data communication and data transmission delay.

 

3.3 Refinements of Functional Model & Stochastic Model

The double-differenced observable is normally used in GPS positioning because of the elimination or reduction of many error sources through differencing. The notion of "short-range" is generally accepted as the distance that distance-dependent errors (or "residual biases") could be ignored in the functional model and the coordinate and integer ambiguity parameters can be estimated. The maximum distance is dependent on the tropospheric delay, ionosphere activity and orbit bias level, and a typical value is 10-15km. However, with the increase in distance between two receivers, the "residual biases" become larger and the fidelity of the functional model will be reduced. If the distance between two GPS receivers is beyond this distance, the distance-dependent errors must be considered in someway if the integer ambiguity needs to be determined. The different modelling methodologies have been developed using multiple reference receivers, e.g. Han & Rizos (1997b), Wanninger (1995), Webster & Kleusberg (1992), Wu (1994), Wübbena et al. (1996). The notion of "medium-range" is then defined for carrier phase-based GPS positioning. The limit of medium-range is between the minimum distance at which the functional model cannot ignore the distance-dependent biases and the maximum distance at which the distance-dependent errors could be modelled accurately enough to fix integer ambiguities. The range is highly environment-related and typically would be between 10km and 100km. If the distance is beyond this medium-range, the integer ambiguity must be fixed using a special procedure, e.g. initialisation at the beginning and then maintain GPS signal tracking during the campaign (Colombo & Rizos, 1996; Han, 1997a; Blewitt, 1989; Dong & Bock, 1989).

The stochastic model is used to describe the error of the measurement apart from its functional model. Although the accuracy of the GPS carrier phase measurement is better than 1% of the cycle and almost independent between epochs and different satellites, the stochastic model cannot be determined based on the measurement noise alone. The stochastic model must consider the misclosure of the functional model and it then becomes environmentally dependent. The importance of the stochastic model can be experimentally demonstrated. For a set of data on a static baseline, the stochastic model could be determined using the residuals after data reduction. The single epoch solution using the estimated stochastic model is much better than the solution using a simple (or conventional) stochastic model (Cross, 1999). However, the stochastic model could only be obtained after intensive data analysis in post-mission mode. For real-time applications, GPS data may be separated into different segments, and the previous data segment can be used to estimate the stochastic model for the current segment (Han, 1997b). The segment length may be assumed to be just a few minutes in length. Real-time stochastic modelling is therefore still a challenging research topic.

The data quality could be judged using the classic data snooping theory (e.g. Baarda, 1977; Förstner, 1983). However, the statistic testing and reliability analysis can only be efficient if the stochastic models are correctly known or well approximated.

3.4 Ambiguity Resolution & Validation Procedures Ambiguity Resolution Techniques Ambiguity resolution (AR) strategy is dependent on the distance between GPS receivers. For short-range applications a number of instantaneous AR techniques have been reported (Han, 1997b; Al-Haifi, et al, 1997). Developments in fast ambiguity resolution algorithms and validation criteria procedures, together with improvements in stochastic modelling and the application of careful quality control procedures, have generally been responsible for this increased level of performance. Ambiguity searching procedures have been developed to significantly reduce the computation load, for example, LSAST (Hatch, 1990); FARA (Frei & Beutler, 1990), Cholesky decomposition method (Euler & Landau, 1992) and LAMBDA (Teunissen, 1994).

Carrier phase-based medium-range GPS kinematic positioning has been reported for baselines several tens of kilometres in length (Wanninger, 1995; Wübbena et al., 1996). The instantaneous AR has also been reported for medium-range GPS kinematic positioning (Han & Rizos, 1997b). Such medium-range performance requires the use of multiple reference stations in order to mitigate the orbit bias, as well as the ionospheric and tropospheric biases. These are exciting developments that will require testing and implementation in operational positioning systems. A joint project between UNSW and the Nanyang Technological University (Singapore) is concerned with establishing a multiple reference system in support of various real-time applications (Rizos et al., 1998). It has been demonstrated that the multiple reference technique could be used to improve the medium-range GPS kinematic positioning and also improve the accuracy of short-range GPS kinematic positioning.

In the case of long-range kinematic positioning several innovative concepts have been reported. Colombo & Rizos (1996) report results of decimetre accuracy navigation over baselines up to a thousand kilometres in length. Although it is not yet possible to resolve ambiguities OTF for baselines of several hundreds of kilometres in length, ambiguity re-initialisation or ambiguity recovery is achievable (Han, 1997a; Han & Rizos, 1995). In other words, if loss-of-lock occurs, the AR algorithm can recover the ambiguities as long as any data "gap" is less than a minute or so. Initial AR must be carried out using traditional techniques, including static initialisation. The sea surface determination using long-range airborne GPS kinematic positioning and Laser Airborne Depth Sounder (LADS) system is discussed by Han et al. (1998).

Validation Criteria and Adaptive Procedure

Using the above mentioned model, the real-valued ambiguities can be estimated and the integer ambiguity search procedure then used to determine the correct integer ambiguity set (that which generates the minimum quadratic form of the residuals). The ratio test of the second minimum and the minimum quadratic form of the residuals is normally used to validate the correct integer ambiguity set (Frei & Beutler, 1990). Euler & Schaffrin (1990) have derived another ratio test, but the critical value is still too conservative and is often experimentally specified as being the value 2 (Wei & Schwarz, 1995), or 1.5 (Han & Rizos, 1996). The testing of the difference between the minimum and second minimum quadratic form of the residuals has been suggested (Tiberius & de Jonge, 1995; Wang, et al., 1998). The other validation criteria based on reliability theory were derived by Han (1997b).

The UNSW strategy uses a series of test to assure the results. This procedure using validation criteria suggested by (ibid, 1997b) assumes that the integer ambiguity set generating the minimum quadratic form of the residuals is correct but detects the outlier of the integer set generating the second minimum quadratic form of the residuals. If this outlier can be detected, the integer set generating the minimum quadratic form of the residuals is considered to be the correct one. On the other hand, the sequence generated by differencing the double-differenced ionospheric delay on L1 and L2 carrier phase can also be used as a validation criteria. If this sequence has a slip (or "jump") at the current epoch, the wrong ambiguity resolution can be confirmed at this epoch. If ambiguity resolution fails and six or more satellites are observed at the current epoch, an adaptive procedure can be applied using a satellite elimination procedure, starting with the one with the lowest elevation, repeating the process until ambiguity resolution is successful. If all possible sets of five or more satellites are combined and the ambiguity test still fails, the ambiguity resolution step is considered to have failed.

3.5 Concluding Remarks

The above discussion is intended as a demonstration of the multi-dimensional approach to QC if the total positioning system is taken into account. It tries to mimic the UKOOA guidelines suggested for real-time, pseudo-range-based DGPS, by dismissing the notion that there is one "magic QC test" that can be implemented. Instead, the different sources of "bad data" and "questionable or unreliable results" are identified and QC/QA tests are suggested (some mathematical in nature, others empirical). The attention to OTF-AR (and in particular to single epoch implementations) is to acknowledge that OTF-AR is the most challenging of GPS data processing problems and that advances in this area will make significant contributions to carrier phase QC. However, unlike the UKOOA guidelines the Chairman does not propose that the tests outlined above should be the "officially" sanctioned ones. The standardisation of QC procedures for carrier phase-based kinematic GPS positioning is still some way off.

The focus on OTF-AR to be implemented in real-time is critical. As no SSG members are actively involved in the development of operational systems, the contribution that can be made in this regard is problematic. Nevertheless, the Chairman has attempted to provide some ideas on how such a system could be implemented. It may take a few more years to thoroughly test and evaluate the appropriate "mix" of QC/QA procedures that would be needed. The Chairman hopes that this report has made a humble contribution to this area of study.

3.6 References Al-Haifi, Y.M., S.J. Corbett and P.A. Cross (1997). Performance Evaluation of GPS Single-Epoch On-The-Fly Ambiguity Resolution. Navigation, Journal of The Institute of Navigation, 44(4):479-487.

Baarda, W. (1977). Measures for the Accuracy of Geodetic Networks. In: "Optimization of Design and Computation of Control Networks", lectures from the symposium held in Sopron, Budapest, Hungary, 4-10 July, 419-426.

Blewitt, G. (1989). Carrier Phase Ambiguity Resolution for the Global Positioning System Applied to Geodetic Baseline up to 2000km. Journal of Geophysical Research, 94(B8), 10187-10203.

Brunner, F.K., H. Hartinger and L. Troyer (1999). GPS Signal Diffraction Modelling: the SIGMA-D Model. Submit to Journal of Geodesy.

Colombo, O.L., C. Rizos and B. Hirsch (1995). Decimetre-Level DGPS Navigation Over Distances of More Than 1000km: Results of the Sydney Harbour Experiment. 4th Int. Conf. on Differential Satellite Navigation Systems, Bergen, Norway, 24-28 April.

Cross, P.A. (1999). Progress In Precise Kinematic GPS Positioning, " GPS Directions 1999" workshop, School of Geomatic Engineering, The University of New South Wales, 8-9 April.

Dong, D.N. And Y. Bock (1989). Global Positioning System Network Analysis with Phase Ambiguity Resolution Applied to Crustal Deformation Studies in California. Journal of Geophysical Research, 94(B4), 3949-3966.

Euler, H.-J. and H. Landau (1992). Fast GPS Ambiguity Resolution On-The-Fly for Real-Time Applications. 6th Int. Geodetic Symp. on Satellite Positioning, Columbus, Ohio, 17-20 March, 650-659.

Euler, H.-J. and B. Schaffrin (1990). On a Measure of the Discernibility between Different Ambiguity Solutions in the Static-Kinematic GPS-Mode. Banff, Canada, 10-13 September. In: K.-P. Schwarz and G. Lachapelle (ed.), Kinematic Systems in Geodesy, Surveying, and Remote Sensing, IAG Symposium No. 107, Springer-Verlag, 285-295.

Förstner, W. (1983). Reliability and Discernability of Extended Gauss-Markov Models. In: F.E. Ackermann (ed.), Photogrammetric Models of Geodetic/Photogrammetric Point Determination With Regard to Outliers and Systematic Errors, Deutsche Geodtische Kommission, Reihe A, Helft Nr. 98, Munich, Germany, 79-103.

Frei, E. and G. Beutler (1990). Rapid Static Positioning Based on the Fast Ambiguity Resolution Approach FARA: Theory and First Results. Manuscripta Geodaetica, 15, 325-356.

Han, S. (1997a). Ambiguity Recovery for GPS Long Range Kinematic Positioning. Navigation, Journal of The Institute of Navigation, USA, Vol 44, No. 2, 257-266.

Han, S. (1997b). Quality Control Issues Relating to Ambiguity Resolution for Real-Time GPS Kinematic Positioning. Journal of Geodesy, 71(6):351-361.

Han, S. and C. Rizos (1995). On-The-Fly Ambiguity Resolution for Long Range GPS Kinematic Positioning. IUGG XXI General Assembly, Colorado, 2-14 July, In: G. Beutler, G.W. Hein, W.G. Melbourne and G. Seeber (ed.): GPS Trends in Precise Terrestrial, Airborne, and Spaceborne Applications, IAG Symposium No. 115, Springer-Verlag, 1996, 290-294.

Han, S. and C. Rizos (1996). Integrated Method for Instantaneous Ambiguity Resolution Using New Generation GPS Receivers. IEEE Position Location & Navigation Symp. PLANS'96, Atlanta, Georgia, 22-26 April, 254-261.

Han S. and C. Rizos (1997a). Multipath Effects on GPS in Mine Environments. Xth International Congress on the International Society for Mine Surveying, Fremantle, Australia, 2-6 November, 447-457.

Han, S. and C. Rizos, (1997b). An Instantaneous Ambiguity Resolution Technique for Medium-Range GPS Kinematic Positioning. 10th Int. Tech. Meeting of the Sat. Div. of the U.S. Inst. of Navigation, Kansas City, Missouri, 16-19 September.

Han, S., C. Rizos and R. Abbot (1998). Flight Testing and Data Analysis of Airborne GPS LADS Survey. . 11th Int. Tech. Meeting of the Sat. Div. of the U.S. Inst. of Navigation, Nashville, Tennessee, 15-18 September, 1211-1221.

Hatch, R.R. (1990). Instantaneous Ambiguity Resolution. In: K.-P. Schwarz and G. Lachapelle (ed.): Kinematic Systems in Geodesy, Surveying and Remote Sensing, IAG Symposium 107, Springer-Verlag, 299-308.

Hartinger, H. and F.K. Brunner (1999). Variance of GPS Phase Observations: The SIGMA-e Model. GPS Solutions, Vol 2, No. 4, 35-43.

Knight, M. and A. Finn (1996). The Impact of Ionospheric Scintillations on GPS Performance. 9th Int. Tech. Meeting of the Sat. Div. of the U.S. Inst. of Navigation, Kansas City, Missouri, 17-20 September, 555-564.

Mertikas, S.P. and C. Rizos (1997). Real-Time Failure Detection in the Carrier Phase Measurements of GPS by Robust and Conventional Kalman Filtering. Journal of Marine Geodesy, 21(1), 41-65.

Landau, H. and H.J. Euler (1992). On-The-Fly Ambiguity Resolution for Precision Differential Positioning. 5th Int. Tech. Meeting of the Sat. Div. of the U.S. Inst. of Navigation, Albuquerque, New Mexico, 22-24 September, 607-613.

Landau, H., C. Pagels and U. Vollath (1995). Development and Implementation of a Centimeter-Accurate Real-Time-Kinematic Positioning System. 8th Int. Tech. Meeting of the Sat. Div. of the U.S. Inst. of Navigation, Palm Springs, California, 12-15 September, 1485-1491.

Langley, R.B. (1994). RTCM SC-104 DGPS standards. GPS World, 5(5), 48-53.

Lapucha, D., R. Barker and Z. Liu (1995). High-Rate Precise Real-Time Positioning Using Differential Carrier Phase. 8th Int. Tech. Meeting of the Sat. Div. of the U.S. Inst. of Navigation, Palm Springs, California, 12-15 September, 1443-1449.

Lin, L.S. and C. Rizos (1997). Use of Multipath Template Technique for Mitigating GPS Pseudo-Range Multipath: Methodology and Test Results. First Trans Tasman Surveyors Conference, Newcastle, Australia, 12-18 April, paper 22, 1-9.

Qiu, W., G. Lachapelle and M.E. Cannon (1995). Ionospheric Effect Modeling for Single Frequency GPS Users. Manuscripta Geodaetica, 20, 96-109.

Rizos, C. (1997). Principles and Practice of GPS Surveying. Monograph 17, School of Geomatic Engineering, The University of New South Wales, ISBN 0-85839--071-X, approx. 560pp.

Rizos C., S. Han, H-Y. Chen and P.C. Goh (1998). Continuously Operating GPS Reference Station Networks: New Algorithms and Applications of Carrier Phase-Based, Medium-Range, Static and Kinematic Positioning. 3rd International Symposium on GPS Technology, Tainan, Taiwan, 10-11 November, 2-4.

Talbot, N.C. (1996). Compact Data Transmission Standard for High-Precision GPS.9th Int. Tech. Meeting of the Sat. Div. of the U.S. Inst. of Navigation, Kansas City, Missouri, 17-20 September, 861-871.

Teunissen, P.J.G. (1994). A New Method for Fast Carrier Phase Ambiguity Estimation. IEEE Position Location & Navigation Symp. PLANS'94, Las Vegas, Nevada, 11-15 April, 562-573.

Tiberius, C.C.J.M. and P.J. de Jonge (1995). Fast Positioning Using the LAMBDA-Method. 4th Int. Conf. on Differential Satellite Navigation Systems, Bergen, Norway, 24-28 April, paper no.30, 8pp.

Wanninger, L. (1993). Effects of the Equatorial Ionosphere on GPS. GPS World, 4(7), 48-54.

Wanninger, L. (1995). Improved Ambiguity Resolution by Regional Differential Modelling of the Ionosphere. 8th Int. Tech. Meeting of the Sat. Div. of the U.S. Inst. of Navigation, Palm Springs, California, 12-15 September, 55-62.

Wang, J., M. Stewart and M. Taskiri (1998). A Discrimination Test Procedure for Ambiguity Resolution On-The-Fly. Journal of Geodesy, 72(11):644-653.

Webster, I. and A. Kleusberg (1992). Regional Modeling of the Ionosphere for Single Frequency Users of the Global Positioning System. Sixth Int. Geodetic Symposium on Satellite Positioning, Columbus, Ohio, 17-20 March, 230-239.

Wei, M. and K.-P. Schwarz (1995). Fast Ambiguity Resolution Using an Integer Nonlinear Programming Method. 8th Int. Tech. Meeting of The Satellite Division of The U.S. Institute of Navigation, Palm Springs, California, 12-15 September, 1101-1110.

Wu, J.T. (1994). Weighted Differential GPS Method for Reducing Ephemeris Error. Manuscripta Geodaetica, 20, 1-7.

Wübbena, G., A. Bagge, G. Seeber, V. Böder and P. Hankemeier (1996). Reducing Distance Dependent Errors for Real-Time Precise DGPS Applications by Establishing Reference Station Networks. 9th Int. Tech. Meeting of the Sat. Div. of the U.S. Inst. of Navigation, Kansas City, Missouri, 17-20 September, 1845-1852.

 

4. APPENDIX

A.1 Address List of SSG 1.154 Members

Assoc. Prof. Chris RIZOS

(Chairperson)

School of Geomatic Engineering,

The University of New South Wales,

Sydney 2052 AUSTRALIA

Ph: +61-2-93854205

Fax: +61-2-93137493

Email: c.rizos@unsw.edu.au

Dr. Hasanuddin ABIDIN

Dept. of Geodetic Engineering,

Institute of Technology Bandung,

Jl. Ganesha 10,

Bandung 40132 INDONESIA

Ph: +62-22-2501645

Fax: +62-22-2505442

Email: hzabidin@indo.net.id

Mr. Jeff BEHR

SCIGN Operations Center,

U.S. Geological Survey,

525 S. Wilson Ave.,

Pasadena, CA 91106 U.S.A.

Ph: +1-818-5837816

Fax: +1-818-5837827

Email: behr@gps.caltech.edu

Assoc. Prof. Elizabeth CANNON

Department of Geomatics Engineering,

The University of Calgary,

2500 University Drive N.W.,

Calgary, Alberta T2N1N4 CANADA

Ph: +1-403-2203593

Fax: +1-403-2841980

Email: cannon@ensu.ucalgary.ca

Mr. Paul COLLINS

Geodetic Research Laboratory,

Department of Geodesy & Geomatics Engineering,

University of New Brunswick,

Fredericton, N.B. E3B5A3 CANADA

Ph: +1-506-4535088

Fax: +1-506-4534943

Email: k4eo@unb.ca

Dr. Roman GALAS

GeoForschungsZentrum, Dept.1,

Telegrafenberg A17,

D-14473 Potsdam GERMANY

Ph: +49-331-2881179

Fax: +49-331-2881111

Email: galas@gfz-potsdam.de

Dr. Shaowei HAN

School of Geomatic Engineering,

The University of New South Wales,

Sydney 2052 AUSTRALIA

Ph: +61-2-93854208

Fax: +61-2-93137493

Email: s.han@unsw.edu.au

Mr. Yuki HATANAKA

Geodetic Observation Center,

Geographical Survey Institute,

1-Kitasato, Tsukuba,

Ibaraki, 305 JAPAN

Ph: +81-298-641111 ext.8643

Fax: +81-298-646864

Email: hata@geos.gsi-mc.go.jp / gps@geos.gsi-mc.go.jp

Dr. Xinxiang JIN

Leica AG,

CH-9435 Heerbrugg

SWITZERLAND

Ph: +41-71-7273367

Fax: +41-71-7274702

Email: Xinxiang.Jin@email.leica.com

Dr. Hansjoerg KUTTERER

Geodetic Institute,

University of Karlsruhe,

Englerstr. 7,

D-76128 Karlsruhe GERMANY

Ph: +49-721-6082309

Fax: +49-721-694552

Email: kutterer@giws4.bau-verm.uni-karlsruhe.de

Mr. Yecai LI

Department of Geomatics Engineering,

The University of Calgary,

2500 University Drive N.W.,

Calgary, Alberta T2N1N4 CANADA

Ph: +1-403-2208794

Fax: +1-403-2841980

Email: yli@acs.ucalgary.ca

Assoc. Prof. Stelios MERTIKAS

Exploration & Positioning Division,

Mineral Resources Engineering Department,

Technical University of Crete,

GR-73100 Chania, Crete GREECE

Ph: +30-821-69327

Fax: +30-821-64802

Email: mertikas@mred.tuc.gr / mertikas@ced.tuc.gr

Assoc. Prof. Peter MORGAN

School of Computing,

Faculty of Information Science & Engineering,

University of Canberra,

PO Box 1 Belconnen,

ACT 2616 AUSTRALIA

Ph: +61-6-2012557

Fax: +61-6-2015041

Email: peterm@ise.canberra.edu.au / pjm@granger.canberra.edu.au

Prof. Stanislaw OSZCZAK

Institute for Geodesy & Photogrammetry,

Olsztyn University of Agriculture & Technology,

Oczapowskiego Str. 1,

10-957 Olsztyn POLAND

Ph: +48-89-5233481

Fax: +48-89-5273908

Email: stan@moskit.art.olsztyn.pl

Dr. William ROBERTS

Quality Engineering & Survey Technology Ltd.,

The Stables,

St Thomas St.,

Newcastle-upon-Tyne NE14LE UNITED KINGDOM

Ph: +44-191-2325977

Fax: +44-191-2300508

Email: roberts@qualityeng.co.uk

Prof. Günter SEEBER

Institute for Geodesy,

University of Hannover,

Nienburgstr. 5,

D-3000 Hannover GERMANY

Ph: +49-511-7622475

Fax: +49-511-7624006

Email: seeber@mbox.ife.uni-hannover.de

Dr. Mike STEWART

School of Spatial Sciences,

Curtin University of Technology,

GPO Box U1987,

Perth 6001 AUSTRALIA

Ph: +61-8-92667600

Fax: +61-8-92662703

Email: stewart@vesta.curtin.edu.au

Dr. Lambert WANNINGER

Geodetic Institute,

Technical University Dresden,

D-01062 Dresden GERMANY

Ph: +49-351-4632852

Fax: +49-351-4637201

Email: wanning@rmhs2.urz.tu-dresden.de

A.2 Bibliography Compiled by A/Prof. Stelios Mertikas Abraham, B. and N. Yatawara (1988). A Score Test for Detection of Time Series Outliers, Journal of Time Series Analysis, 9(2), 109-119.

Abraham, B. and A. Chuang (1989). Outlier Detection and Time Series Modeling, Technometrics, 31(2), 241-247.

Anderson, T.W. (1984). An Introduction to Multivariate Statistical Analysis, John Wiley, New York, second edition.

Baarda, W. (1968). A Testing Procedure for Use in Geodetic Networks, The Netherlands Geodetic Commission, New Series, 2(5), Delft.

Bansal, R.K. and P. Papantoni-Kazakos (1989). Outlier-Resistant Algorithms for Detecting a Change in a Stochastic Process, IEEE Transactions on Information Theory, 35(3), 521-535.

Barnett, V. and T. Lewis (1994). Outliers in Statistical Data, John Wiley and Sons, New York, third edition.

Bassevile, M. (1981). Edge Detection Using Sequential Methods for Change in Level-Part II: Sequential Detection of Change, IEEE Transactions on Acoustics, Speech and Signal Processing, Vol. ASSP-29, No. 1, 32-50.

Bassevile, M. and A. Benveniste, eds (1986). Detection of Abrupt Changes in Signals and Dynamical Systems, Lecture Notes in Control and Information Sciences, LNCIS No. 77, Springer-Verlag, New York.

Basseville, M. and I.V. Nikiforov (1993). Detection of Abrupt Changes: Theory and Applications, P T R Prentice Hall, Englewood Cliffs, New Jersey.

Basseville, M., A. Benveniste, G. Moustakides and A. Rougee (1987). Detection and Diagnosis of Changes in the Eigenstructure of Nonstationary Multivariate Systems, Automatica, 23(3), 479-489.

Basilevsky, A. (1983). Applied Matrix Algebra in the Statistical Sciences, North Holland, New York.

Bastos, L. and H. Landau (1988). Fixing Cycle Slips in Dual-Frequency Kinematic GPS-Applications Using Kalman Filtering, Manuscripta Geodeatica, 13, 249-256.

Bernardo, J.M. and A.F. Smith (1994). Bayesian Theory, John Wiley & Sons, New York, Chichester, Brisbane, Toronto, Singapore.

Biacs, Z.W., E.J. Krakiwsky, and D. Lapucha (1990). Reliability Analysis of Phase Observation in GPS Baseline Estimation, Journal of Surveying Engineering, American Society of Civil Engineers, 116(4), 204-224 .

Boos, D.D. (1980). A New Method for Constructing Approximate Confidence Intervals from M Estimates, Journal of the American Statistical Association, 75(369), 142-145.

Brown, R.G. (1983). Introduction to Random Signal Analysis and Kalman Filtering, John Wiley and Sons, New York.

Brown, R.G. (1992). A baseline GPS RAIM Scheme and a Note on the Equivalent of Three RAIM Methods, NAVIGATION, Journal of The Institute of Navigation, 39(3).

Brown, R.G. and P.Y.C. Hwang (1992). Introduction to Random Signals and Applied Kalman Filtering, John Wiley and Sons, second edition, New York.

Brumback, B.D. and M.D. Srinath (1987). A Chi-Square Test for Fault-Detection in Kalman Filters, IEEE Transactions on Automatic Control, AC-32(6), 552-554, June.

Bryson, A.E. and L.J. Henrikson (1968). Estimation Using Sampled Data Containing Sequentially Correlated Noise, Journal of Rocket and Spacecraft, 5(6), 662-665.

Cannon, M.E., K.P. Schwarz, M. Wei, and D. Delikaraoglou (1992). A Consistency Test of Airborne GPS Using Multiple Monitor Stations, Bulletin Geodesique, 66, 2-11.

Chan, T.F., G.H. Goloub and R.J. Le Veque (1983). Algorithms for Computing the Sample Variance: Analysis and Recommendations, The American Statistician, 37, 242-247.

Chang, C.B. and K.P. Dunn (1979). On GLR Detection and Estimation of Unexpected Inputs in Linear Discrete Systems, IEEE Transactions on Automatic Control, AC-24(3), 499-501.

Chernick, M.R., D.J. Downing and D.H. Pike (1982). Detecting Outliers in Time Series Data, Journal of the American Statistical Association, 77(380), 743-747.

Chien, T.T. and M.B. Adams (1976). A Sequential Failure Detection Technique and its Application, IEEE Transactions on Automatic Control, Short Papers, 750-757, October.

Chu, K.A.C. (1973). Estimation and Decision for Linear Systems with Elliptical Random Processes, IEEE Transactions on Automatic Control, Short Papers, 499-505, October.

Cipra, T. and R. Romera (1991). Robust Kalman Filter and its Application in Time Series Analysis, Kybernetika, 27(6), 481-494.

Chang, T.C. and F.F. Gan (1995). A Cumulative Sum Control Chart for Monitoring Process Variance, Journal of Quality Technology, 27(2), 109-119 .

Chow, E.Y and A.S. Willsky (1984). Analytical Redundancy and the Design of Robust Failure Detection Systems, IEEE Transactions on Automatic Control, AC-29(7), 603-613.

Crowder, S.V. (1989). Design of Exponentially Weighted Moving Average Schemes, Journal of Quality Technology, 21(3), 155-162.

Csorgo, H. and L. Horvath (1988). Nonparametric Methods for Change Point Problems, In Handbook of Statistics (P.R. Krishnaiah, C.R. Rao, eds), Vol.7, Elsevier, New York, 403-425.

Da, R. (1995). A New Failure Detection Approach and Its Applications to GPS Autonomous Integrity Monitoring, IEEE Transactions on Aerospace and Electronic Systems, 31(1), 499-506.

Deckert, J.C., M.N. Desai, J.J. Deyst, and A.S. Willsky (1977). F-8 DFBW Sensor Failure Identification Using Analytic Redundancy, IEEE Transactions on Automatic Control, AC-22(5), 795-803.

Duncan, A.J. (1986). Quality Control and Industrial Statistics, Irwin, Homewood, Illinois, fifth edition.

Embrechts, P., A.M. Herzberg and A.C.K. Ng (1986). An Investigation on Andrews' Plots to Detect Period and Outliers in Time Series Data, Communications in Statistics, Simulation, 15(4), 1027-1051.

Ershov, A.A. and S.Sh. Liptser (1978). Robust Kalman Filter in Discrete Time, Translated from Avtomatika i Telemekhanika, 3, 60-69, 359-367.

Fitzgerald, R.J. (1971). Divergence of the Kalman filter, IEEE Transactions on Automatic Control, AC-16, 736.

Frank, P.M. (1990). Fault Diagnosis in Dynamic Systems Using Analytical and Knowledge-Based Redundancy - A Survey and Some New Results, Automatica, 26, 459-474.

Gan, F.F. (1991). An Optimal Design of CUSUM Quality Control Charts, Journal of Quality Technology, 23(4), 279-286.

Gan, F.F. (1993). The Run Length Distribution of a Cumulative Sum Control Chart, Journal of Quality Technology, 25(3), 205-207.

Gan, F.F. (1994). Design of Optimal Exponential CUSUM Control Charts, Journal of Quality Technology, 26(2), 109-124.

Gan, F.F. (1995). Joint Monitoring of Process Mean and Variance Using Exponentially Weighted Moving Average Control Charts, Technometrics, 37(4), 446-453.

Gan, F.F. and K.P. Choi (1994). Computing Average Run Lengths for Exponential CUSUM Schemes, Journal of Quality Technology, 26(2), 134-143.

Gao, Y. (1992). A Robust Quality Control System for GPS Navigation and Kinematic Positioning, Ph.D. Dissertation, Department of Geomatics Engineering, The University of Calgary, Canada.

Gelb, A. (ed, 1974). Applied Optimal Estimation, The M.I.T. Press, Massachusetts Institute of Technology, Cambridge, Massachusetts.

Hampel, F.R., E.M. Ronchetti, P.J. Rousseeuw and W.A. Stahel ( 1986). Robust Statistics: The Approach Based on Influence Functions, John Wiley and Sons, New York.

Hawkins, D.M. (1980). Identification of Outliers, Monographs on Applied Probability & Statistics, Chapman & Hall, London.

Hawkins, D.M. (1981). A Cusum for a Scale Parameter, Journal of Quality Technology, 13(4), 228-231.

Hawkins, D.M. (1987). Self-Starting Cusum Charts for Location and Scale, The Statistician, 36, 299-315.

Hawkins, D.M. (1992). A Fast Accurate Approximation for Average Run Lengths of CUSUM Control Charts, Journal of Quality Technology, 24(1), 37-43.

Hawkins, D.M. (1993). Robustification of Cumulative Sum Charts by Winsorization, Journal of Quality Technology, 25(4), 248-261, October.

Hinkley, D.V. (1970). Inference About the Change Point in a Sequence of Random Variables, Biometrika, 57(1), 1-17.

Hinkley, D.V.(1971). Inference About the Change-Point From Cumulative Sum-Tests, Biometrika, 58(3), 509-523.

Hunter, J.S. (1986). The Exponentially Weighted Moving Average, Journal of Quality Technology, 18(4), 203-210.

Isermann, R. (1984). Process Fault Detection Based on Modelling and Estimation Methods, Automatica,20, 387-404.

Jazwinski, A.H. (1968). Limited Memory Optimal Filtering, IEEE Transactions on Automatic Control, Short Papers, 558-563, October.

Jia, M. and X. Ding (1996). On the Selection of Deformation Models and Its Impact on Deformation Analysis, Proceedings of the FIG 8th International Symposium on Deformation Measurements, Hong Kong, 25-28 June.

Johnson, R.A. and D.W. Wichern (1988). Applied Multivariate Statistical Analysis, Prentice-Hall, Inc., Englewood Cliffs, New Jersey, second Edition.

Kemp, K.W. (1961). The Average Run Length of the Cumulative Sum Chart When a V-Mask is Used, Journal of the Royal Statistical Society, B-23, 149-153.

Kerr, T.H. (1977). Real-Time Failure Detection: A Nonlinear Optimization Problem That Yields a Two-Ellipsoid Overlap Test, Journal of Optimization Theory and Applications, 22(4), 509-536, August.

Kerr, T.H. (1980). Statistical Analysis of a Two-Ellipsoid Overlap Test for Real-Time Failure Detection, IEEE Transactions on Automatic Control, AC-25(4), 762-773, August.

Kerr, T.H. (1982). False Alarm and Correct Detection Probabilities over a Time Interval for Restricted Classes of Failure Detection Algorithms, IEEE Transactions on Information Theory, IT-28(4), 619-631.

Kerr, T.H. (1987). Decentralized Filtering and Redundancy Management for Multisensor Navigation, IEEE Transactions on Aerospace and Electronic Systems, AES-23(1), 83-118, corrections in AES-23(3), 412, May 1987.

Kersen, P. and L. Kurz (1976). Robustized Vector Robbins-Monro Algorithm with Applications to M-Interval Detection, Information Sciences, 11, 121-140.

Ketel, M. and L. Kurt (1994). Robust Sequential MIPA Array Processor With Dependent Sampling, Journal of the Acoustical Society of America, 95(6), 3409-3418.

Kinnaert, M., R. Hanus and Ph. Arte (1995). Fault Detection and Isolation for Unstable Linear Systems, IEEE Transactions on Automatic Control, 40(4), 740-742.

Kligene, N. and L. Telksnis (1984). Methods of Detecting Instants of Random Process Properties, Translated from Avtomatika i Telemekhanika, 10, 5-56.

Krishnaiah, P.R. and C.R. Rao (eds.) (1988). Handbook of Statistics 7: Quality Control and Reliability, North-Holland, Amsterdam, New York, Oxford.Kullback, S. (1959). Information Theory and Statistics, Wiley, New York.

Lorden, G. (1971). Procedures for Reading a Change in Distribution, Annals of Mathematical Statistics, 42(6), 1897-1908.

Lu, G. (1991). Quality Control for Differential Kinematic GPS Positioning, University of Calgary Surveying Engineering Report, Number 20042, August.

Lucas, J.M. (1985). Cumulative Sum (CUSUM) Control Schemes, Communications in Statistics: Theory and Methods, 14(11), 2689-2704.

Lucas, J.M. and R.B. Crosier (1982). Robust Cusum: A Robustness Study for Cusum Quality Control Schemes, Communications in Statistics: Theory and Methods, 11(23), 2669-2787.

Lucas, J.M. and R.B. Crosier (1982). Fast Initial Response for CUSUM Quality-Control Schemes: Give your CUSUM a Head Start, Technometrics, 24(3), 199-205.

MacGregor, J.F. and T.J. Harris (1993). The Exponentially Weighted Moving Variance, Journal of Quality Technology, 25(2), 106-118.

Martin, R.D. (1972). Robust Estimation of Signal Amplitude, IEEE Transactions on Information Theory, IT-18(5), 596-606, September.

Martin, R.D. and C.J. Masreliez (1975). Robust Estimation via Stochastic Approximation, IEEE Transactions on Information Theory, IT-21(3), 263-271, May.

Masreliez, C.J. and R.D. Martin (1977). Robust Bayesian Estimation for the Linear Model and Robustifying the Kalman Filter, IEEE Transactions on Automatic Control, AC-22(3), 361-371.

Masreliez, C.J. (1975). Approximate Non-Gaussian Filtering with Linear State and Observation Relations, IEEE Transactions on Automatic Control, Short Papers, 107-110, February.

Mehra, R.K. and J. Peschon (1971). An Innovations Approach to Fault Detection and Diagnosis in Dynamic Systems, Automatica, 7, 637-640.

Meinhold, R.J. and N.D. Singpurwalla (1989). Robustification of Kalman Filter Models, Journal of the American Statistical Association, 84(406), Theory and Methods, 479-486.

Mertikas, S.P. (1994). The Description of Accuracy Using Conventional and Robust Estimates of Scale, Marine Geodesy, 42, 251-269.

Minkler, G. and J. Minkler (1993). Theory and Application of Kalman Filtering, Magellan Book Company, Palm Bay, Florida, USA.

Mironovski, L.A. (1980). Functional Diagnosis of Dynamic Systems: A Survey, Automation and Remote Control, 41, 1122-1143.

Mond, C.E.D. and R.V. Lenth (1987). A Robust Confidence Interval for Location, Technometrics, 29(2), 211-219.

Muirhead, C.R. (1986). Distinguishing Outlier Types in Time Series, Journal of The Royal Statistical Society, 48(1), 39-47.

Quesenburry, C.P. (1986). Screening Outliers in Normal Process Control Data with Uniform Outliers, Journal of Quality Technology, 18(4), October.

Quesenburry, C.P. (1991). SPC Q Charts for Start-Up Processes and Short or Long Runs, Journal of Quality Technology, 23(3), 213-224.

Quesenburry, C.P. (1995). On Properties of Q Charts for Variables, Journal of Quality Technology, 27(3), 184-203.

Page, E.S. (1954a). Continuous Inspection Schemes, Biometrika, 41, 100-115.

Page, E.S. (1954b). Control Charts for the Mean of a Normal Population, Journal Royal Statistical Society, B-16(1), 131-135.

Page, E.S. (1955). A Test for a Change in Parameter Occurring at an Unknown Point, Biometrika, 43, 523-527.

Papoulis, A. (1984). Probability, Random Variables and Stochastic Processes, McGraw-Hill company, New York, second edition.

Patton, R.J. and J. Chen (1991). A Review of Parity Space Approaches to Fault Diagnosis, Proceedings of SAFEPROCESS'91, Baden-Baden, Germany, pp. 239-256.

Pau, L.F. (1981). Failure Diagnosis and Performance Monitoring, Control and Systems Theory Series Monographs and Textbooks, Dekker, New York.

Pena, D. and I. Guttman (1989). Optimal Collapsing of Mixture Distributions in Robust Recursive Estimation, Communications in Statistics, Theory and Methods, 18(3), 817-833.

Pervan, B.S., C. Cohen and B. Parkinson (1994). Integrity Monitoring for Precision Approach Using Kinematic GPS and Ground-Based Pseudolite, NAVIGATION, Journal of The Institute of Navigation, 41(2).

Piercy, N.P. (1992). Sensor Failure Estimators for Detection Filters, IEEE Transactions on Automatic Control, 37(10), 1553-1557.

Poljak, B.T. and J.Z. Tsypkin (1980). Robust Identification, Automatica, Vol. 16, pp. 53-63.

Rao, C.R. (1973). Linear Statistical Inference and its Applications, John Wiley and Sons, New York, second edition.

Reynolds, R.D. (1990). Robust Estimation of Covariance Matrices, IEEE Transactions on Automatic Control, 35(9), 1047-1051, September.

Rollins, D.K. and J.F. Davis (1993). Gross-Error Detection When Variance-Covariance Matrices are Unknown, AI Chemical Engineering Journal, 39(8), 1335-1341.

Rousseeuw, P.J. and A.M. Leroy (1987). Robust Regression and Outlier Detection, John Wiley & Sons, New York, Chichester, Brisbane, Toronto, Singapore.

Ryan, T.P. (1989). Statistical Methods for Quality Improvement, John Wiley and Sons, New York.

Roes, K.C.B. , R.J.M.M. Does and Y. Schurink (1993). Shewart-Type Control Charts for Individual Observations, Journal of Quality Technology, 25(3), 188-198.

Sacks, J. and D. Ylvisaker (1972). A Note on Huber's Robust Estimation of a Location Parameter, The Annals of Mathematical Statistics, 43(4), 1068-1075.

Saif, M. and Y. Guan (1993). A New Approach to Robust Fault Detection and Identification, IEEE Transactions on Aerospace and Electronic Systems, 29(3), 685-695.

Salzmann, M. (1993). Least Squares Filtering and Testing for Geodetic Navigation Applications, Ph.D. Dissertation, Technical University of Delft, Delft Geodetic Computing Centre.

Salzmann, M. and P.J.G. Teunissen (1989). Quality Control in Kinematic Data, Processing, In Deutsche Gesellschaft fuer Ortung and Navigation, Land Vehicle Navigation, Verlang TUV Rheinland, Kln, pp. 355-366.

Salzmann, M. and P.J.G. Teunissen (1990). Detection and Modelling of Coloured Noise for Kalman Filter Applications, Proceedings of the IAG International Symposium 107 on Kinematic Systems in Geodesy, Surveying and Remote Sensing, Springer-Verlag, N.Y., pp. 201-217.

Schwarz, K.P., M.E. Cannon and R.V.C. Wong (1989). A Comparison of GPS Kinematic Models for the Determination of Position and Velocity Along a Trajectory, Manuscripta Geodetica, 14, 345-353.

Selin, I. (1968). Detection Theory, Princenton University Press, Princenton, New Jersey.

Siegmund, D. (1975). Error Probabilities and Average Sample Number of the Sequential Probability Ratio Test, Journal Royal Statistical Society, B-37, 394-401.

Stoodley, K.D.C. and M. Mirnia (1978). The Automatic Detection of Transients, Step Changes and Slope Changes in the Monitoring of Medical Time Series, The Statistician, 28(3), 163-171.

Stahel, W. and S. Weisberg (eds,1991). Directions in Robust Statistics and Diagnostics, Springer-Verlag, New York.

Strang, G. (1980). Linear Algebra and its Application, Academic Press, New York, second edition.

Stratton, D.A. and R.F. Stengel (1993). Robust Kalman Filter Design for Predictive Wind Shear Detection, IEEE Transactions on Aerospace and Electronic Systems, 29(4), 1185-1193.

Tanaka, M. and T. Katayama (1987). Robust Kalman Filter for Linear Discrete Time System with Gaussian Sum Noises, International Journal of Systems Science, 18(9), 1721-1731.

Tanaka, M. and T.Katayama (1988). Robust Fixed-Lag Smoother for Linear Systems Including Outliers in the System and Observation Noises, International Journal of Systems Science, 19(11), 2243-2259.

Teunissen, P.J.G. (1990). Some Aspects of Real-time Model Validation Techniques for Use in Integrated Systems, Proceedings of the IAG International Symposium 107 on Kinematic Systems in Geodesy, Surveying and Remote Sensing, Springer-Verlag, N.Y., pp. 191-200.

Teunissen, P.J.G. (1990). Quality Control in Integrated Navigation Systems, Proceedings of the IEEE PLANS, Las Vegas, 20-23 March, pp. 158-165.

Teunissen, P.J.G. and M. Salzmann (1989). A Recursive Slippage Test for Use in State-Space Filtering, Manuscripta Geodaetica, 14(6), 383-390.

Tiku, M.L., W.Y. Tan and N. Balakrishnan (1986). Robust Inference, Marcel Dekker, Inc., New York, Textbooks & Monographs on Statistics, Vol. 71.

Tsui, C.C. (1994). A General Failure Detection, Isolation and Accommodation System with Model Uncertainty and Measurement Noise, IEEE Transactions on Automatic Control, 39(11), 2318-2321.

Turkey, A.A. (1989). Fault Detection and Diagnosis in Dynamic Systems- A Survey, No. 14 Report, Computer and Automation Institute, Hungarian Academy of Sciences.

Tsai, C. and L. Kurz (1983). An Adaptive Robustizing Approach to Kalman Filtering, Automatica, 19, 279-288.

Tsay, R.S. (1988). Outliers, Level Shifts and Variance Changes in Time Series, Journal of Forecasting, 7, 1-10.

Tukey, J.W. (1960). A Survey of Sampling From Contaminated Distributions, In Contributions to Probability and Statistics, I. Olkin (ed), Stanford University Press, Stanford, California, pp. 448-485.

Vance, L.C. (1986). Average Run Lengths of Cumulative Sum Control Charts for Controlling Normal Means, Journal of Quality Technology, 18(3), 189-193.

Van Dyke, K.L. (1995). Fault Detection and Exclusion Performance Using GPS and CLONASS, NAVIGATION, Journal of The Institute Of Navigation, 42(4).

Van Trees, H.L. (1968). Detection, Estimation and Modulation Theory, Part I, John Wiley and Sons, New York.

Wallace, D.L. (1959). Bounds on Normal Approximations to Student's and the Chi-Square Distributions, Annals of Mathematical Statistics, 30, 1121-1130.

Wang, Y.J. and K.K. Kubik (1993). Robust Kalman Filter and its Geodetic Applications, Manuscripta Geodaetica, 18, 349-354.

Warren, D.J. and J.B. Thomas (1991). Asymptotically Robust Detection and Estimation for Very Heavy-Tailed Noise, IEEE Transactions on Information Theory, Vol. 37, No. 3, pp. 475-481.

Wei, M., D. Lapucha and H. Martell (1990). Fault Detection and Estimation in Dynamic Systems, Proceedings of the IAG International Symposium 107 on Kinematic Systems in Geodesy, Surveying and Remote Sensing, Springer-Verlag, New York.

Willsky, A.S. (1976). A Survey of Design Methods for Failure Detection in Dynamic Systems, Automatica, 12, 601-611.

Willsky, A.S. (1986). Detection of Abrupt Changes in Dynamic Systems, Charter 2 in Detection of Abrupt Changes in Signals and Dynamic Systems, edited by M. Basseville and A. Benveniste, Control and Information Sciences No. 77, Springer-Verlag, Berlin.

Willsky, A.S., E.Y. Chow, S.B. Gershwin, C.S. Greene, P.K. Houpt and A.L. Kurkjian (1980). Dynamic Model-Based Techniques for the Detection of Incidents on Freeways, IEEE Transactions on Automatic Control, AC-25(3), 347-360, June.

Willsky, A.S. (1980). Failure Detection in Dynamic Systems, AGARD Lecture Series No 109 Fault Tolerance Design and Redundancy Management Techniques, Chapter 2.

Willsky, A.S., J.J. Deyst and B.S. Crawford (1975). Two Self-Test Methods Applied to an Inertial System Problem, Journal of Spacecraft, 12, 434-437, July.

Willsky, A.S. and H.L. Jones (1976). A Generalized Likelihood Ratio Approach to the Detection and Estimation of Jumps in Linear Systems, IEEE Transactions on Automatic Control, Short Papers, 108-112, February.

Wu, N.E. and Y.Y. Wang (1995). Robust Failure Detection with Parity Check on Filtered Measurements, IEEE Transactions on Aerospace and Electronic Systems, 31(1), 489-491.

Zhang, X.J. (1989). Auxiliary Signal Detection in Fault Detection and Diagnosis, Lecture Notes in Control and Information Sciences, No. 134, Springer-Verlag, Berlin.